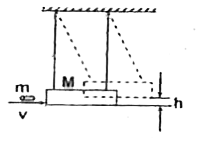
A bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
To solve the problem, we will follow these steps:
Step 1: Calculate the initial momentum of the bullet
The initial momentum of the bullet can be calculated using the formula:
Momentum=mass×velocity
Given:
- Mass of the bullet m=0.012kg
- Velocity of the bullet v=70m/s
Calculating the initial momentum:
Initial momentum=m×v=0.012kg×70m/s=0.84kg m/s
Step 2: Apply the conservation of momentum
After the bullet strikes the block, they move together with a common velocity V′. The total mass after the collision is m+M, where M=0.4kg is the mass of the block.
Using the conservation of momentum:
m⋅v=(m+M)⋅V′
Substituting the values:
0.84=(0.012+0.4)⋅V′
0.84=0.412⋅V′
Now, solving for V′:
V′=0.840.412≈2.04m/s
Step 3: Calculate the height to which the block rises
The kinetic energy just after the collision is converted into potential energy as the block rises. The loss in kinetic energy is equal to the gain in potential energy.
The formula for kinetic energy (KE) is:
KE=12(m+M)V′2
Calculating the kinetic energy:
KE=12⋅0.412⋅(2.04)2
KE≈12⋅0.412⋅4.1616≈0.857J
The potential energy (PE) at height h is given by:
PE=(m+M)gh
Setting the kinetic energy equal to the potential energy:
0.857=(0.412)⋅9.8⋅h
Now, solving for h:
h=0.8570.412⋅9.8≈0.212m
Step 4: Calculate the heat produced in the block
The heat produced is equal to the loss in kinetic energy during the collision.
Initial kinetic energy of the bullet:
KEinitial=12mv2=12⋅0.012⋅(70)2
KEinitial=12⋅0.012⋅4900=29.4J
Final kinetic energy after the collision:
KEfinal=12(m+M)V′2=12⋅0.412⋅(2.04)2
KEfinal≈0.857J
The heat produced is:
Heat=KEinitial−KEfinal=29.4−0.857≈28.54J
Final Answers:
- Height to which the block rises: 0.212 m
- Amount of heat produced in the block: 28.54 J
The initial momentum of the bullet can be calculated using the formula:
Momentum=mass×velocity
Given:
- Mass of the bullet m=0.012kg
- Velocity of the bullet v=70m/s
Initial momentum=m×v=0.012kg×70m/s=0.84kg m/s
After the bullet strikes the block, they move together with a common velocity V′. The total mass after the collision is m+M, where M=0.4kg is the mass of the block.
m⋅v=(m+M)⋅V′
Substituting the values:
0.84=(0.012+0.4)⋅V′
0.84=0.412⋅V′
Now, solving for V′:
V′=0.840.412≈2.04m/s
The kinetic energy just after the collision is converted into potential energy as the block rises. The loss in kinetic energy is equal to the gain in potential energy.
KE=12(m+M)V′2
Calculating the kinetic energy:
KE=12⋅0.412⋅(2.04)2
KE≈12⋅0.412⋅4.1616≈0.857J
PE=(m+M)gh
Setting the kinetic energy equal to the potential energy:
0.857=(0.412)⋅9.8⋅h
Now, solving for h:
h=0.8570.412⋅9.8≈0.212m
The heat produced is equal to the loss in kinetic energy during the collision.
KEinitial=12mv2=12⋅0.012⋅(70)2
KEinitial=12⋅0.012⋅4900=29.4J
KEfinal=12(m+M)V′2=12⋅0.412⋅(2.04)2
KEfinal≈0.857J
Heat=KEinitial−KEfinal=29.4−0.857≈28.54J
- Height to which the block rises: 0.212 m
- Amount of heat produced in the block: 28.54 J
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Additional Exercises
3 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - higher order thinking skills
10 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Advanced Problems For Competitions
20 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A and B are two particles having the same mass m. A is moving along X-axis with a speed of 10ms−1 and B is at rest. After undergoing a perfectly elastic collision with B, particle A gets scattered through an angle of 30∘. What is th edirection of motion of B, and the speeds of A and B, after the collision?
View SolutionTwo balls A and B of masses 0.3 kg and 0.2 kg respectively are moving along positive X-axis and negaive X-axis with velocities 2.0 m / s. They collide and thereafter move in the directions opposite to their original directions. Find the velocities of A and B after collision. Also, calculate total K.E. of the ball before and after collision.
View SolutionTwo identical 5 kg blocks are moving with same speed of 2m/s towards eachother along a frictionless horizontal surface. The two blocks collide, stick together and come to rest. Consider the two blocks as a system. Caluculate work done by (i) external forces (ii) internal forces.
View SolutionAssertion : Internal energy of an ideal gas does not depend upon volume of the gas.
Reason : This is because internal energy of ideal gas depends only on temperature of gas.
View SolutionA wooden block of mass 0.9 kg is suspended from the ceiling of a room by thin wires. A bullet of mass 0.1 kg moving horizontally with a speed of 10 ms^(-1) strikes the block and sticks to it. What is the height to which the block rises ? Take g = 10 ms^(-2) :
View SolutionA bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
View Solution0.012kg द्रव्यमान की कोई गोली 70ms−1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है । गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए ।
View Solution0.012 किग्रा द्रव्यमान कि कोई गोली 70 मीटर/सेकण्ड कि क्षैतिज चाल से चलते हुए 0.4 किग्रा द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरंत ही विरामावस्था में आ जाती है। गुटके को छत से पतली तारो द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है। ? गुटके के पैदा हुई ऊष्मा कि मात्रा भी अनुमान लगाइए।
View SolutionA block of wood of mass 0.5 kg is suspended by means of a thin wire. A bullet of mass 0.020 kg is fired horizontally in the plane of the block with a velocity of 100ms−1. If the bullet gets stuck inside the block, then calculate the height by which the system rises (g=9.8ms−2). Calculate the amount of heat produced in the block.
View SolutionA bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Estimate the loss in kinetic energy.
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
Initial speed of the bullet is
View SolutionA bullet of mass 0.012kg and horizontal speed 70 ms^(-1) strikes a block of wood of mass 0.4kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionA bullet of mass 0.012kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionA bullet of mass 0.012kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionA bullet of mass 0.012 kg and horizontal speed 70ms^(-1) strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View Solution