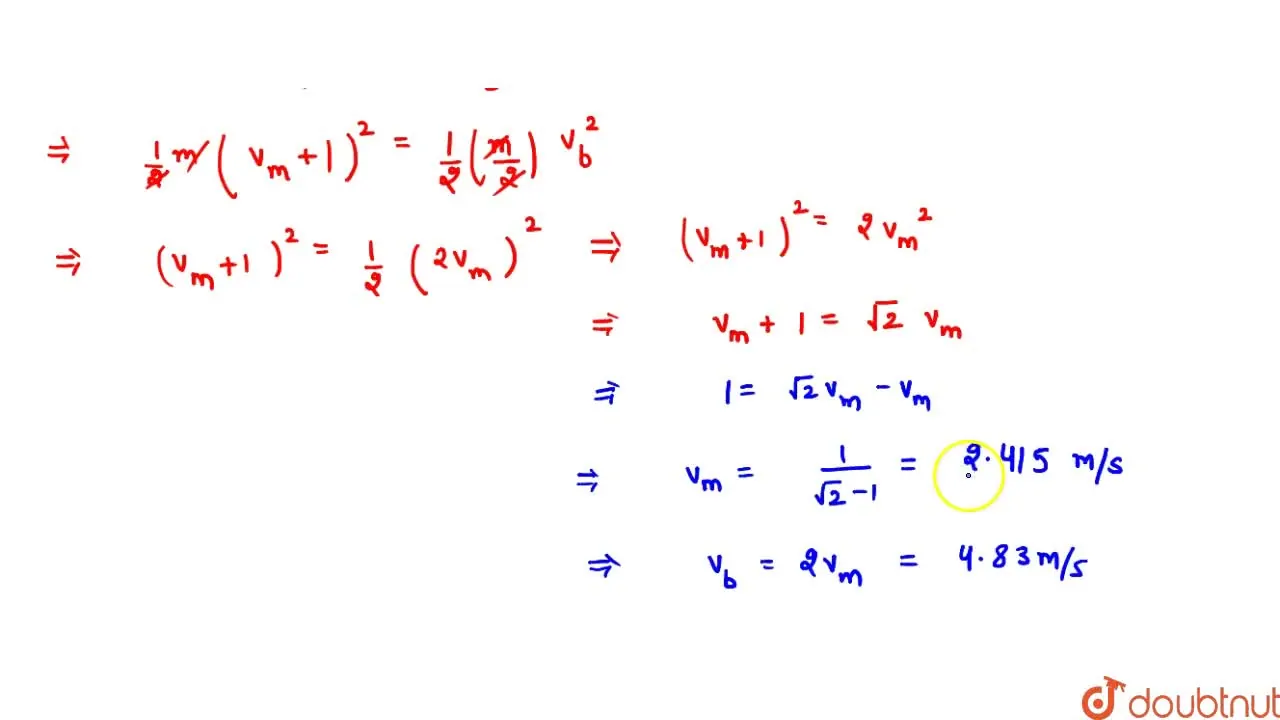A running man has half the KE that a body of half his mass has. The man speeds up by 1.0ms−1 and then has the same energy as the boy. What were the original speeds of the man and the boy?
Let mass of man =m,
mass of boy =m2
Let velocity of man be v1 and velocity of boy =v2
As per question, KE of man =12 KE of boy
=12mv21=12×12m2v22
∴v1=v2/2 ...(i)
When speed of man becomes (v1+1), KE becomes equal.
12m(v1+1)2=12⋅m2v22=m4(2v1)2=mv21
v1+1=√2v1=2×2.415=4.830m/s
Related Playlists
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems27videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.54videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions2videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A man running has half the kinetic energy of a boy of half his mass. The man speeds up by 1 m/s and then has kinetic energy as that of the boy. What were the original speeds of man and the boy ?
View SolutionA man running has half the kinetic energy of a boy of half his mass. The man speeds up by 1ms−1 and then has KE as that of the boy. What was the original speed of man?
View SolutionA man who is running has half the kinetic energy of a boy of half his mass. The man speeds up by 1 ms−1 and then has the same kinetic energy as the boy. The original speed of the boy was:
View SolutionA man who is running has half the kinetic energy of a boy of half his mass. The man speeds up by 1 ms−1 and then has the same kinetic energy as the boy. The original speed of the boy was:
View SolutionA father racing his son has half the kinetic energy of the son, who has half the mass of the father. The father speeds up by 1.0 m/s and then has the same kinetic energy as the son. What are the original speeds of (a) the father and (b) the son ?
View SolutionA running man has the same kinetic energy as that of a boy of half his mass. The man speed up by 2ms−1 and the body changes his speed by xms−1 so that the kinetic energies of the boy and the man are again equal. Then x in ms−1 is
View SolutionA running man has the same kinetic energy as that of a boy of half his mass. The man speed up by 2ms−1 and the boy changes his speed by xms−1 so that the kinetic energies of the boy and the man are again equal. Then x in ms−1 is
View SolutionA running man has the same kinetic energy as that of a boy of half his mass. The man speeds up by 2ms−1 and the boy changes his speed by xms−1 so that the kinetic energies of the boy and the man are again equal. Then x in ms−1 is
View SolutionA man has twice the mass of a boy and has half the kinetic energy of the boy. The ratio of the speeds of the man and the boy must be
View SolutionA lady running on the road has kinetic energy that is half of that of girl . The girl's mass is half of the lady's mass. The lady increases her speed y m/s and then has the same energy as of girl . Calculate the original speeds of the lady and the girl .
View Solution