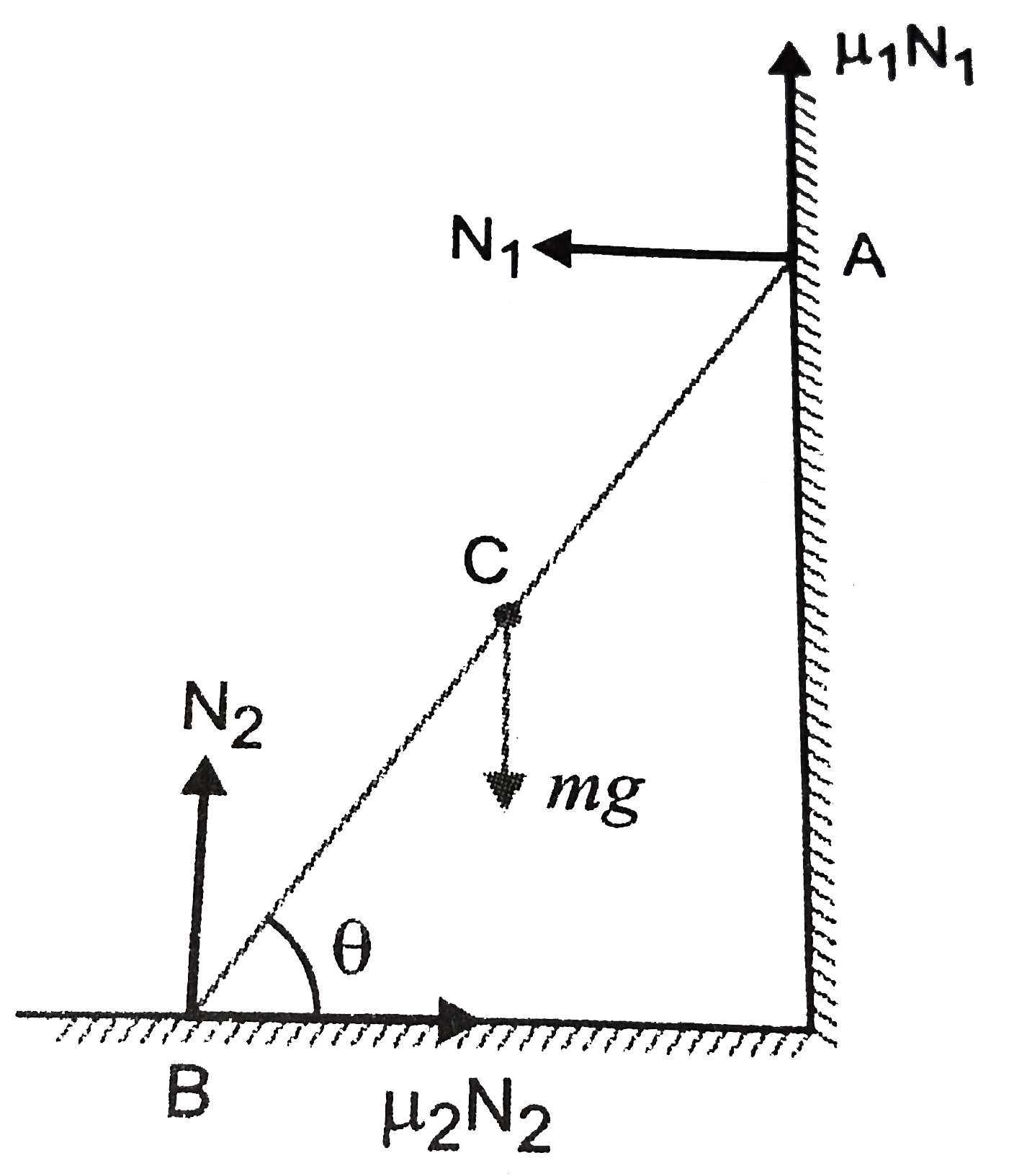
In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle $θ$ with the horizontal floor. The coefficient of friction between the wall and the ladder is $μ_{1}$ and that between the floor and the ladder is $μ_{2} .$ the normal reaction of the wall on the ladder is $N_{1}$ and that of the floor is $N_{2} .$ if the ladder is about to slip. than

A

$μ_{1} = 0, μ_{2} \neq 0 and N_{2} tan θ = m g / 2$

B

$μ_{1} \neq 0, μ_{2} = 0 and N_{1} tan θ = m g / 2$

C

$μ_{1} \neq 0, μ_{2} \neq 0 and N_{2} = \frac{m g}{1 + μ_{1} μ_{2}}$

D

$μ_{1} = 0, μ_{2} \neq 0 and N_{1} tan θ = \frac{m g}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c,d

For maximum equilibrium $μ_{2}$ can never be zero When $μ_{1} = 0$ we have
$N_{1} = μ_{2} N_{2}$ …(i)
and $N_{2} = m g$ …(ii)
As ladder is in equilibrium so taking moments of force about point $B$ we have
$m \frac{g (L)}{2} cos θ = N_{1} L sin θ$
or $N_{1} = \frac{m g}{2 tan θ}$ or $N_{1} tan θ = \frac{m g}{2}$
When $μ_{1} \neq 0$ and there is equilibrium of ladder
then $μ_{1} N_{1} + N_{2} = m g$ ...(iii)
and $μ_{2} N_{2} = N_{1}$ ...(iv)
Putting (iv) in (iii) we get $μ_{1} μ_{2} N_{2} + N_{2} = m g$
or $N_{2} = \frac{m g}{1 + μ_{1} μ_{2}}$
.

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ladder of length $l$ and mass $m$ is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is $μ$ . The angle $θ$ at which the ladder will stay in equilibrium is
A $θ = {tan}^{- 1} (μ)$
B $θ = {tan}^{- 1} (2 μ)$
C $θ = {tan}^{- 1} (\frac{μ}{2})$
Dnone of these
Question 2 - Select One
A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is

A50N
B $50 \sqrt{3} N$
C $\frac{60}{\sqrt{3}} N$
D100N
Question 3 - Select One
A ladder $5 m$ long rests against a vertical wall. If its top slides down at the rate of $10 c m / sec$ , then, when the foot of the ladder is $4 m$ away from the wall, the angle between the floor and the ladder is decreasing at the rate of
A $\frac{π}{4} radians / sec$ .
B $\frac{4}{π} radians / sec$ .
C $(0.025) radians / sec$ .
D $\frac{π}{6} radians / sec$ .

PRADEEP-LAWS OF MOTION-JEE (Main and Advanced)/ Medical Entrance Special

Home
Ask Doubt
Profile