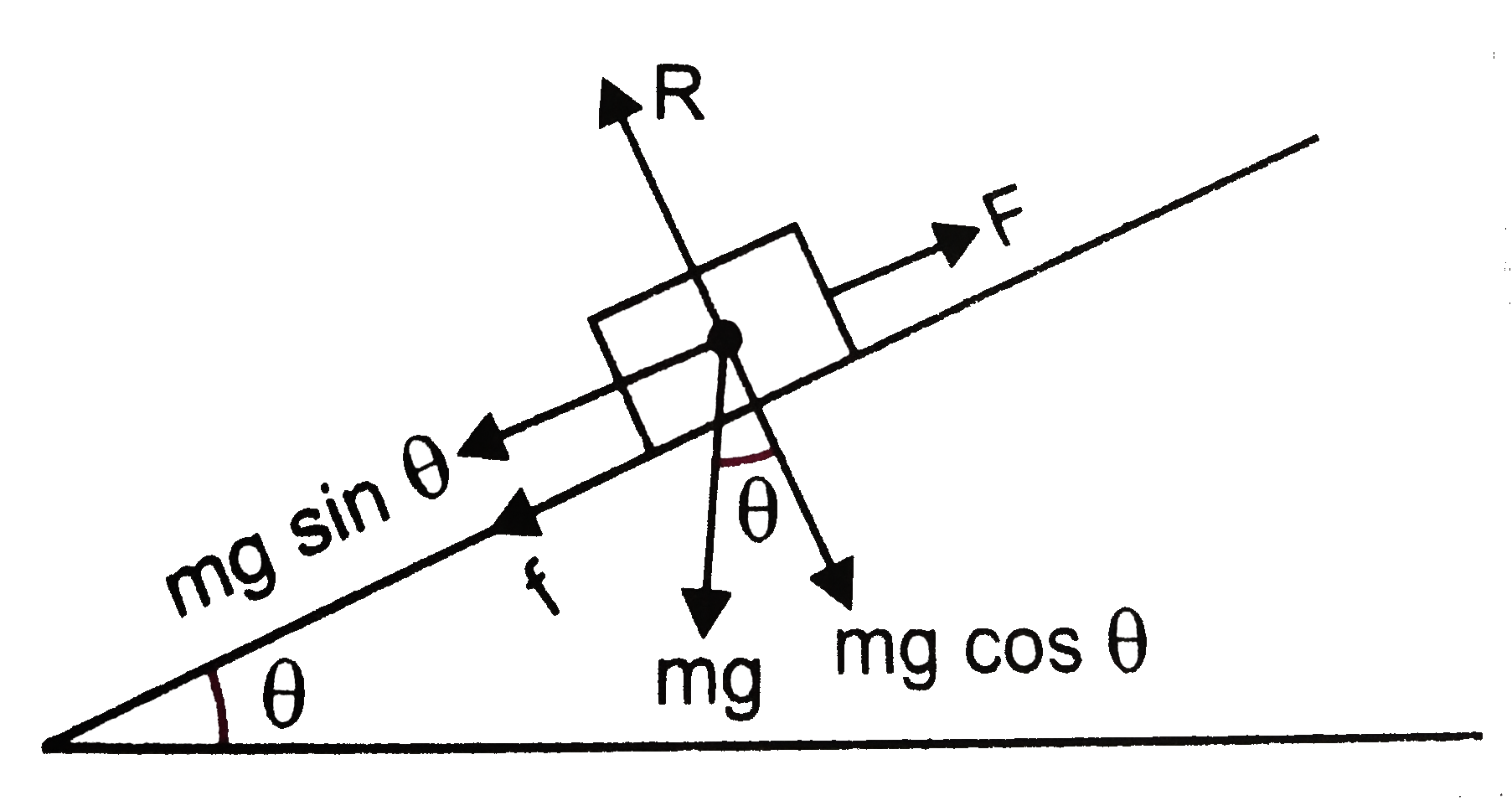
A mass of 200 kg is placed on a rough inclined plane of angle . If coefficient of limiting friction is , find the least forces in newton , acting parallel to the plane (i) to keep the mass from sliding down (ii) to move the mass up the plane.
To solve the problem, we need to determine the forces acting on a mass of 200 kg on a rough inclined plane at an angle of 30 degrees, given that the coefficient of limiting friction is 1√3. We will find the least force required to (i) keep the mass from sliding down and (ii) to move the mass up the plane.
1. Calculate the gravitational force acting down the incline:
Fgravity=mgsinθ
Where g (acceleration due to gravity) is approximately 9.81m/s2.
Fgravity=200×9.81×sin(30∘)=200×9.81×12=981N
2. Calculate the normal force:
Fnormal=mgcosθ
Fnormal=200×9.81×cos(30∘)=200×9.81×√32≈200×9.81×0.866≈1697.56N
3. Calculate the maximum frictional force:
Ffriction=μFnormal=1√3×1697.56≈979.59N
4. Set up the equilibrium equation:
To keep the mass from sliding down, the applied force F must balance the gravitational force minus the frictional force:
F+Ffriction=Fgravity
Rearranging gives:
F=Fgravity−Ffriction=981−979.59≈1.41N
(ii) To move the mass up the plane:
1. Set up the equation for moving up:
When moving up the incline, the applied force must overcome both the gravitational force and the frictional force:
F=Fgravity+Ffriction
F=981+979.59≈1960.59N
Final Answers:
- (i) The least force to keep the mass from sliding down is approximately 1.41 N.
- (ii) The least force to move the mass up the plane is approximately 1960.59 N.
Fgravity=mgsinθ
Where g (acceleration due to gravity) is approximately 9.81m/s2.
Fgravity=200×9.81×sin(30∘)=200×9.81×12=981N
Fnormal=mgcosθ
Fnormal=200×9.81×cos(30∘)=200×9.81×√32≈200×9.81×0.866≈1697.56N
Ffriction=μFnormal=1√3×1697.56≈979.59N
To keep the mass from sliding down, the applied force F must balance the gravitational force minus the frictional force:
F+Ffriction=Fgravity
Rearranging gives:
F=Fgravity−Ffriction=981−979.59≈1.41N
When moving up the incline, the applied force must overcome both the gravitational force and the frictional force:
F=Fgravity+Ffriction
F=981+979.59≈1960.59N
- (i) The least force to keep the mass from sliding down is approximately 1.41 N.
- (ii) The least force to move the mass up the plane is approximately 1960.59 N.
Similar Questions
A body of mass 10 kg is placed on an inclined surface of angle 30∘ . If coefficient of limiting friction is 1/√3 , find the inclined plane. Force is being exerted parallel to the inclined plane
 .
.
View SolutionA mass of 100kg is resting on a rough inclined plane of angle 30∘ If the coefficient of friction is 1/√3 find the greatest and the least forces that acting parallel to the plane in both cases just maintain the mass in equilibrium .
View Solution
Knowledge Check
A body weighing 20 kg just slides down a rough inclined plane that rises 5 in 12. The coefficient of friction is
A0.46B4.6C0.52D0.12A body of mass 10 kg is lying on a rough plane inclined at an angle of 30∘ to the horizontal and the coefficient of friction is 0.5. the minimum force required to pull the body up the plane is
A914 NB91.4 NC9.14 ND0.914 NA body of mass 2 kg is placed on rough horizontal plane. The coefficient of friction between body and plane is 0.2 Then,
 Abody will move in forward direction if F = 5 NBbody will be move in backward direction with acceleration 0.5m/s2 if force F = 3NCif F = 3N, then body will be in rest conditionDBoth a and c are correct
Abody will move in forward direction if F = 5 NBbody will be move in backward direction with acceleration 0.5m/s2 if force F = 3NCif F = 3N, then body will be in rest conditionDBoth a and c are correct
A metal block of mass 0.5 kg is placed on a plane inclined to the horizontal at an angle of 30∘. If the coefficient of friction is 0.2, what force must be applied (i) to just prevent the block from sliding down the inclined plane (ii) to just move the block up the inclined plane and (iii) to move it up the inclined plane with an acceleration of 20cms−2?
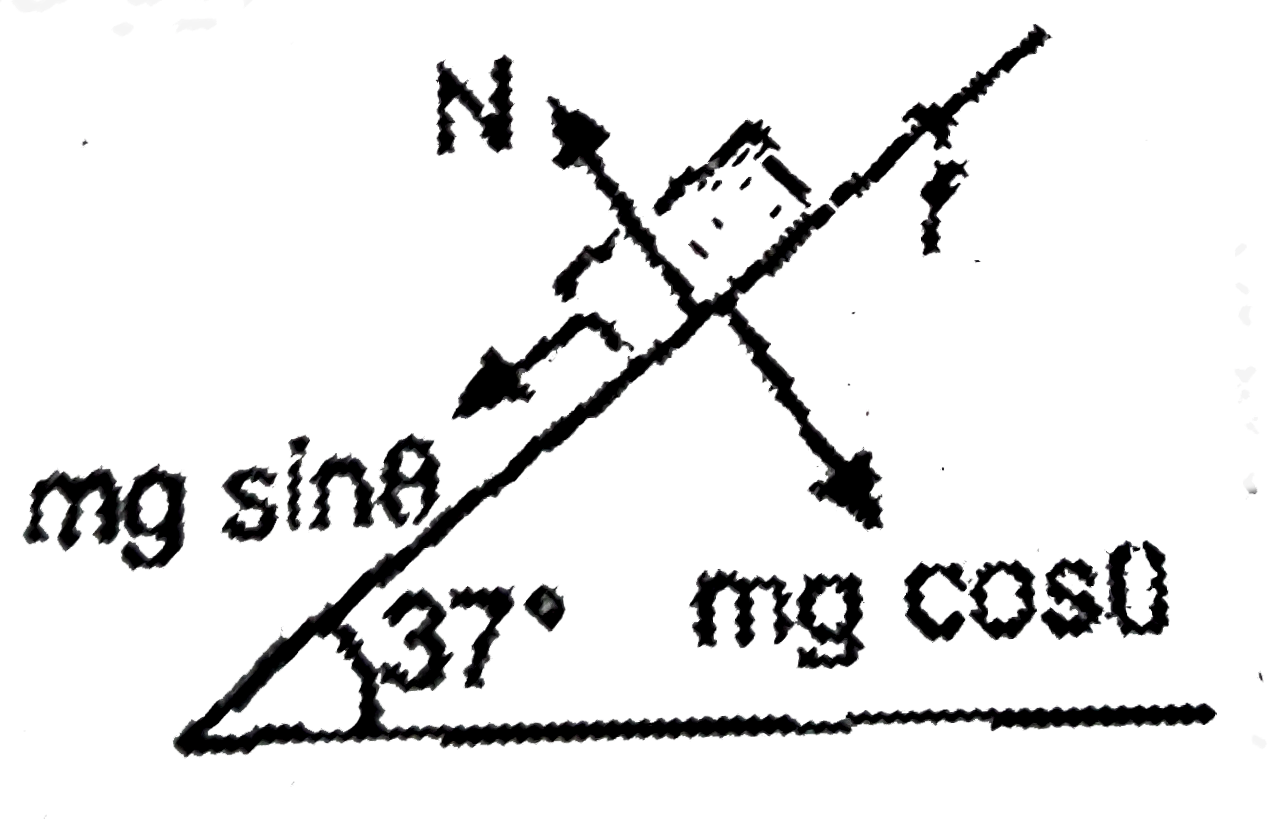
View SolutionA block of mass 3 kg slides on a rough fixed inclined plane of 37∘ angle having coefficient of friction 0.5. find the resultant force exerted by plane on the block.
View SolutionA block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block

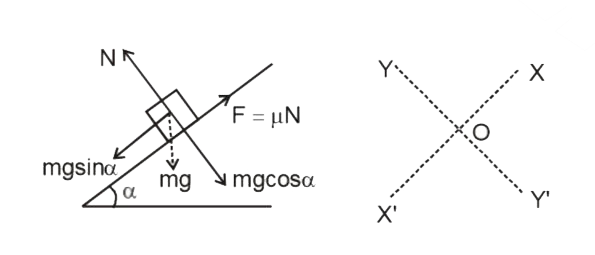
View SolutionA 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is

View Solution

