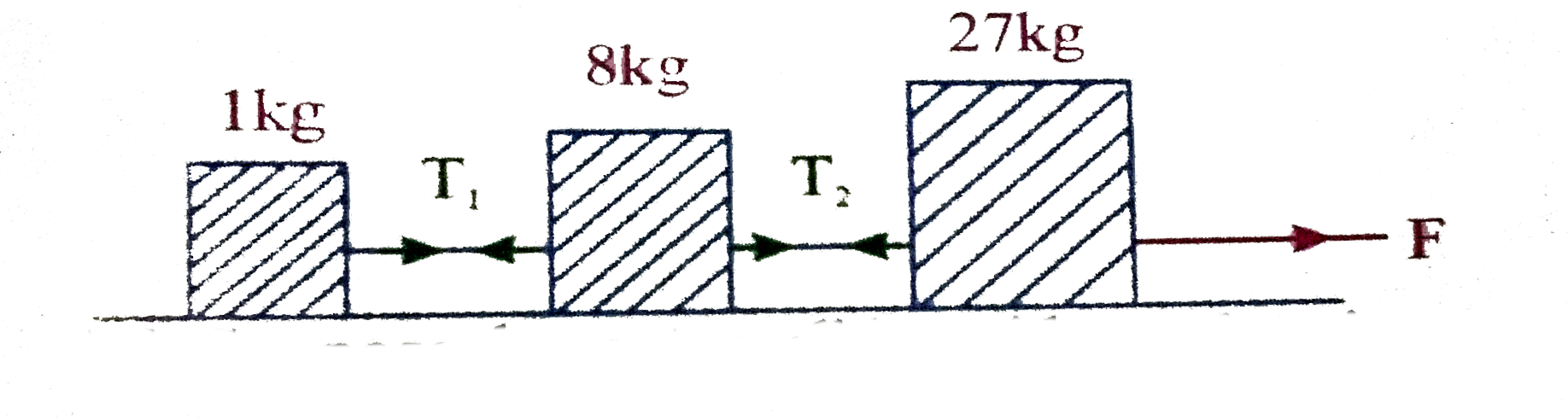
Four blocks of the same mass m connected by cords are pulled by a force F on a smooth horizontal surface as shown in Determine the tensions T1T2 and T3 in the cords.
To solve the problem of finding the tensions T1,T2, and T3 in the cords connecting four blocks of mass m being pulled by a force F on a smooth horizontal surface, we can follow these steps:
Step 1: Understand the System
We have four blocks of mass m connected by cords. When a force F is applied to the first block, all blocks will accelerate together with the same acceleration A.
Step 2: Calculate the Total Mass
The total mass of the system is:
M=4m
Step 3: Apply Newton's Second Law to the Entire System
According to Newton's second law:
F=M⋅A
Substituting the total mass:
F=4m⋅A
From this, we can solve for the acceleration A:
A=F4m
Step 4: Analyze the Forces on the Last Block
For the last block (Block 4), the only force acting on it is the tension T3:
T3=m⋅A
Substituting for A:
T3=m⋅F4m=F4
Step 5: Analyze the Forces on the Third Block
For the third block (Block 3), the forces acting on it are T2 (pulling it forward) and T3 (pulling it backward):
T2−T3=m⋅A
Substituting for A and T3:
T2−F4=m⋅F4m
This simplifies to:
T2−F4=F4
Thus:
T2=F4+F4=F2
Step 6: Analyze the Forces on the Second Block
For the second block (Block 2), the forces acting on it are T1 (pulling it forward) and T2 (pulling it backward):
T1−T2=m⋅A
Substituting for A and T2:
T1−F2=m⋅F4m
This simplifies to:
T1−F2=F4
Thus:
T1=F2+F4=2F4+F4=3F4
Summary of Tensions
The tensions in the cords are:
T1=3F4,T2=F2,T3=F4
We have four blocks of mass m connected by cords. When a force F is applied to the first block, all blocks will accelerate together with the same acceleration A.
The total mass of the system is:
M=4m
According to Newton's second law:
F=M⋅A
Substituting the total mass:
F=4m⋅A
From this, we can solve for the acceleration A:
A=F4m
For the last block (Block 4), the only force acting on it is the tension T3:
T3=m⋅A
Substituting for A:
T3=m⋅F4m=F4
For the third block (Block 3), the forces acting on it are T2 (pulling it forward) and T3 (pulling it backward):
T2−T3=m⋅A
Substituting for A and T3:
T2−F4=m⋅F4m
This simplifies to:
T2−F4=F4
Thus:
T2=F4+F4=F2
For the second block (Block 2), the forces acting on it are T1 (pulling it forward) and T2 (pulling it backward):
T1−T2=m⋅A
Substituting for A and T2:
T1−F2=m⋅F4m
This simplifies to:
T1−F2=F4
Thus:
T1=F2+F4=2F4+F4=3F4
The tensions in the cords are:
T1=3F4,T2=F2,T3=F4
Topper's Solved these Questions
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Very short answer questions
Explore 73 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Long Answer Questions
Explore 16 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:solved examples
Explore 104 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
Similar Questions
Knowledge Check
Four blocks of same mass connected by cords are pulled by a force F on a smooth horizontal surface as shown in figure. The tensions T1,T2 and T3 will be
F←MT1−MT2−MT3−MAT1=14,T2=32,T3=14BT1=14,T2=12F,T3=12FCT1=34,T2=12F,T3=14FDT1=34,T2=12F,T3=12FFour blocks of same mass connected by cords are pulled by a force F on a smooth horizontal surface as shown in figure. The tensions T1,T2 and T3 will be
F←MT1−MT2−MT3−MAT1=14,T2=32,T3=14BT1=14,T2=12F,T3=12FCT1=34,T2=12F,T3=14FDT1=34,T2=12F,T3=12FFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
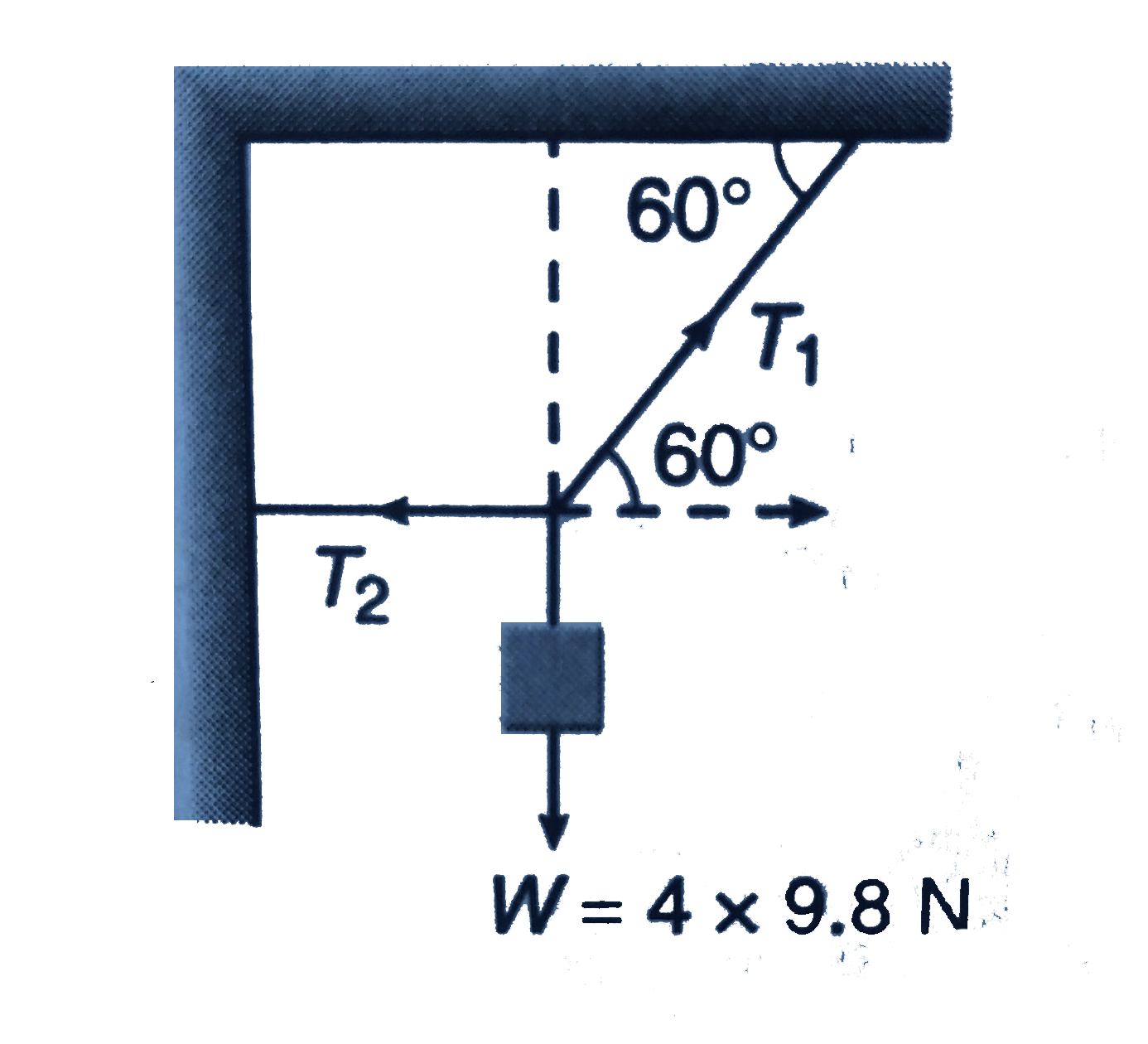
Determine the tensions T1 and T2 in the strings as shown in figure.
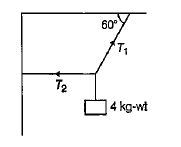
View SolutionA block of mass 10 kg is suspended with two strings as shown in the fig. Find the tensions T1andT2 in the two string.
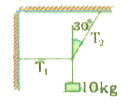
View SolutionThree blocks connected together by strings are pulled along a horizontal surface by applying a force F.IfF=36N What is the tension T2 ?.
 .
.
View SolutionConsider three blocks of masses m1,m2,m3 interconnected by strings which are pulled by a common force F on a frictionless horizontal table as in the figure. The tension T1andT2 are also indicated

a) T2>T1 if m2>m1
b) T2=T1 if m2=m1
c) T2>T1 always
d) acceleration of the system=Fm1+m2+m3
View SolutionConsider three blocks of masses m1,m2,m3 interconnected by strings which are pulled by a common force F on a frictionless horizontal tabel as in the figure. The tension T1 and T2 are also indicated
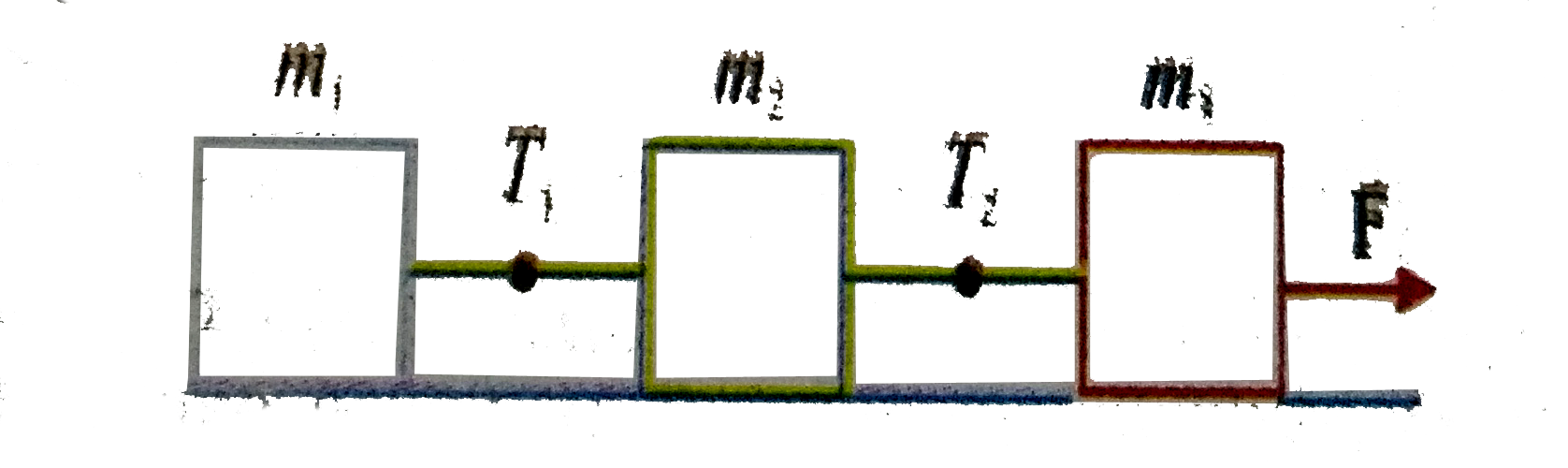 .
.
a) T2>T1 if m2>m1
b)T2=T1 if m2=m1 , c) T2>T1 always
d) acceleration of the system Fm1+m2+m3 .
View Solution