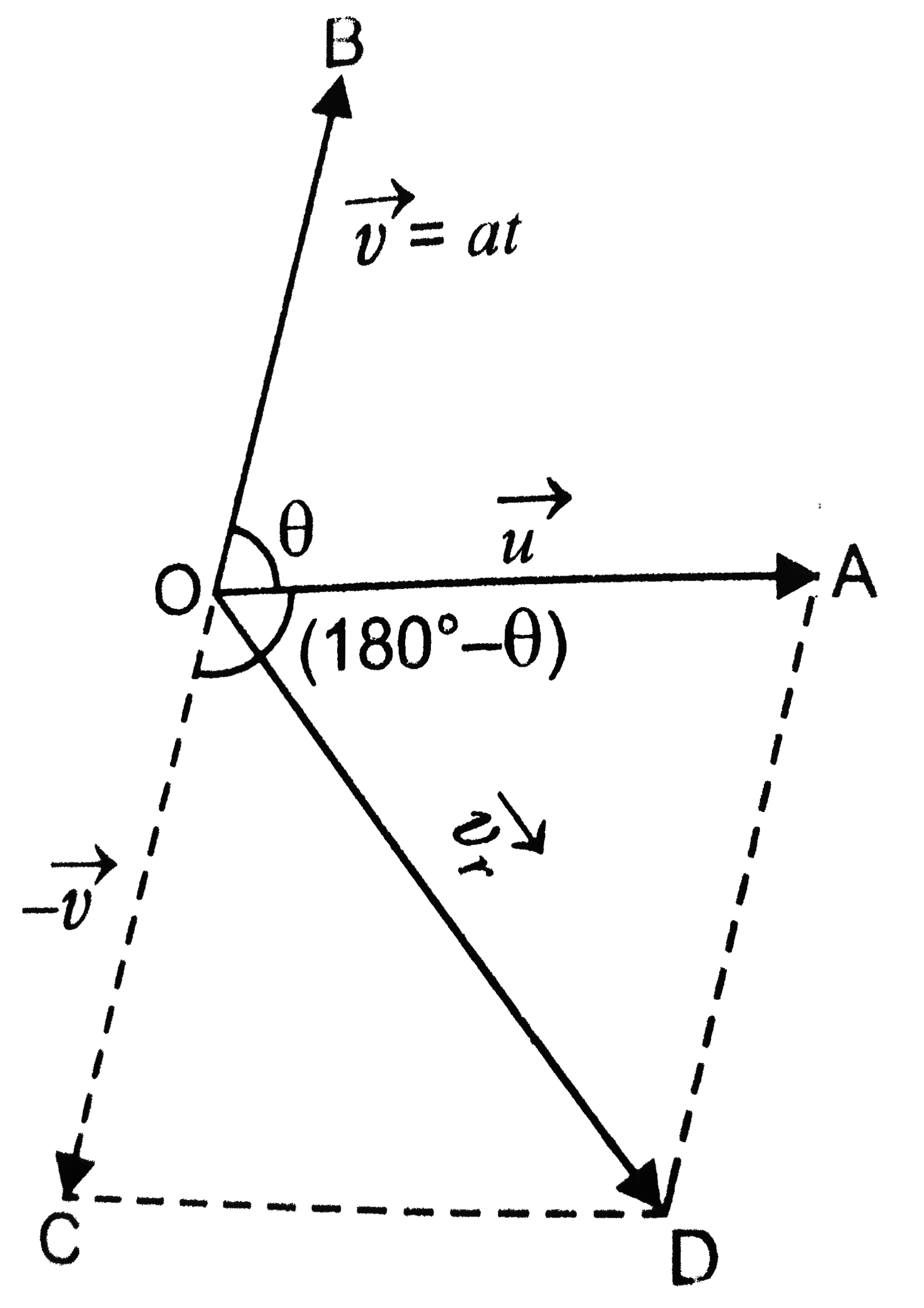
Two cacar starts together from the asme point and move along two straight lines inclined at an angle θ, one moving with velocity (u) and the other from rest with a uniform acceleration (a). Show that the least relative velocity between then is usinθ and it occurs after a time t=(ucosθ)/a.
Let the first car be moving with uniform velocity (u) along (OA) and the second car be moving with uniform acceleration (a) along OB, Fig. 2. (c ) . 98.
After (t) seconds the velocity of second car,
v=at ltbRgt Relative velocity of first car w.r..t the second
car is →vr=→u−→v=→u+(−→v)
−−→OA+−−→OC=−−→OD
 .
.
Magniude of →vr is given by
v2r=u2+v2+2uvcos(1802−θ)
vr=[u2_a2t2−2uatcosθ]1/2
vr is minimum if dvrdt=0
(dv_r)/(dt) = 1/2 ( u^2+a^2t^2-2 u at cos theta) ^(-1//2)<br>xx 9 2 A^2 t- 2 u a cos theta)=0<br>Hence, 2 a^2 t- 2 u a u a cos theta =0<br>or t= ( u cos theta)/a<br> :. v_r = [ u^2 +a^2 xx ( u^2 cos^2 theta)/a^2 -2ua ( ucos theta)/a xx cos theta]^(1//2).<br> [ u^2 -u^2 cos^2 hteta]^(1//2)<br>= u sin theta (Proved).
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 Problems for practice
Explore 45 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 Multiple choice
Explore 10 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:2 Problems for practice
Explore 36 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
Two particles start simulataneously from the same point and moves along two straight lines inclined at angle α, one with uniform velocity v0 and other from the rest with uniform acceleration, a0. After how much time their relative velocity is minimum and what is it equal to?
View SolutionA body A starts from rest and moves with a uniform acceleration along a straight line. Another body B has some initial velocity and moves with larger acceleration than that of A. The correct velocity time graphs
View Solution
Knowledge Check
Two particles start simultaneously from the same point and move along two straight lines. One with uniform velocity v and other with a uniform acceleration a. if α is the angle between the lines of motion of two particles then the least value of relative velocity will be at time given by
AvasinαBvacosαCvatanαDvacotαTwo particles start simultaneously from a point with equal velocities v each along two straight inclined at 60∘. Find their relative velocity
AVB2VCV2D3VA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
A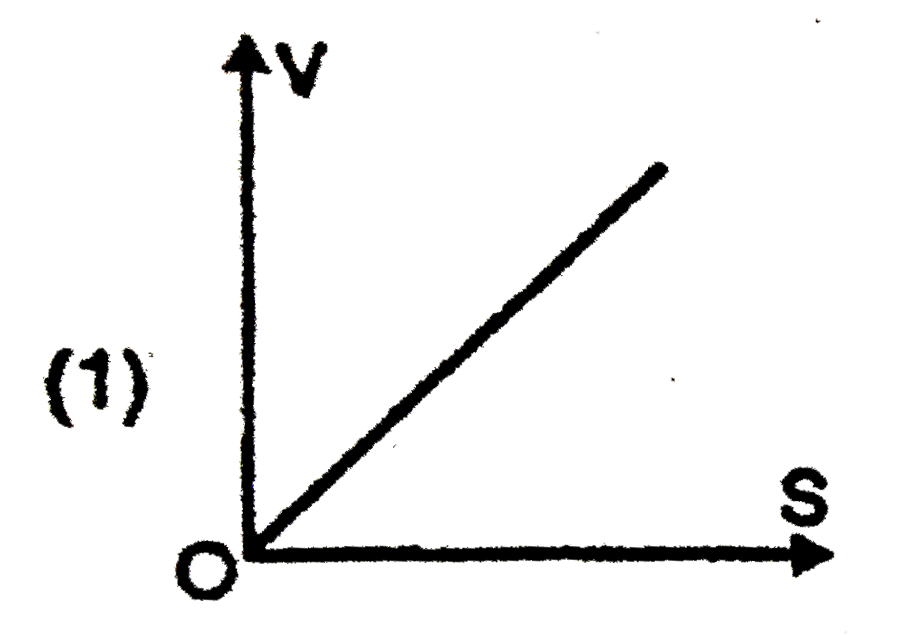 B
B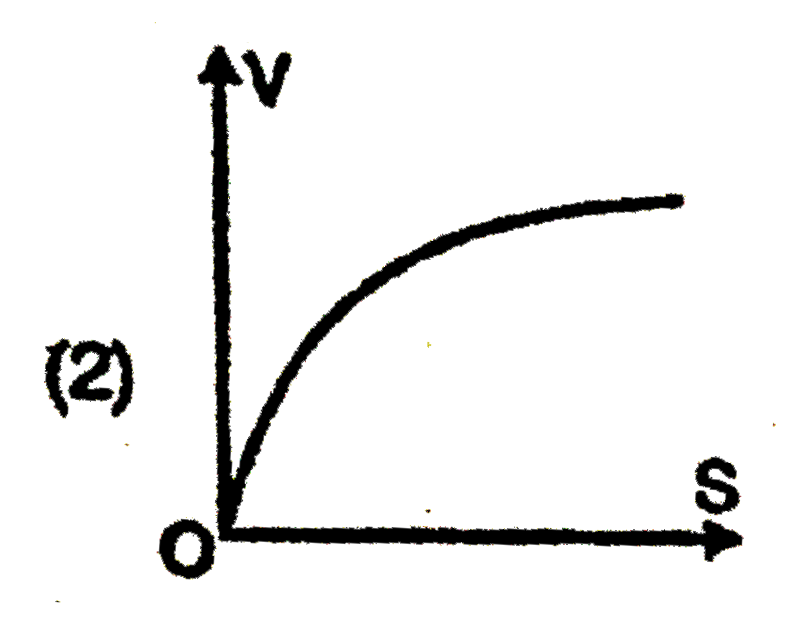 C
C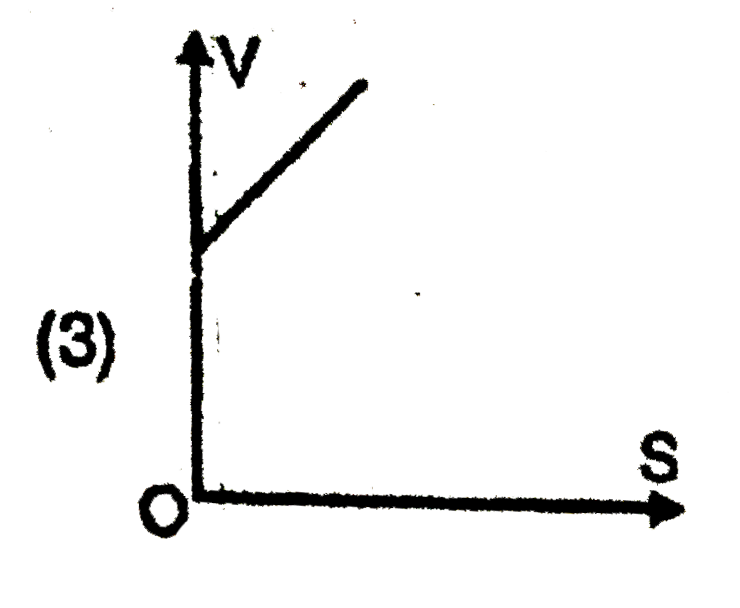 D
D
At time t = 0, two bodies A and B at the same point. A moves with constant velocity υ and B starts from rest and moves with constant acceleration. Relative velocity of B w.r.t. A when the bodies meet each other is
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
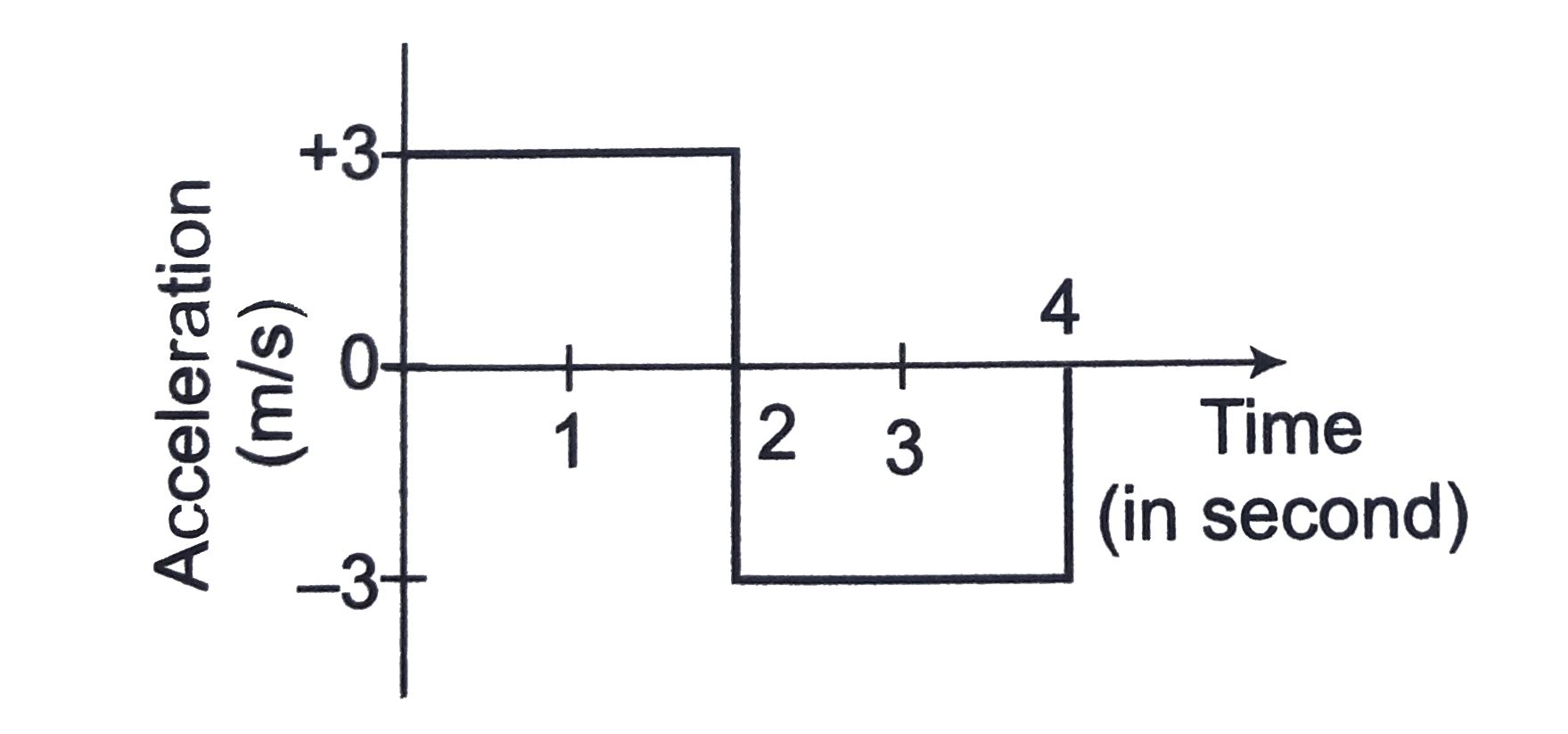
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionTwo particles move in the same straight line starting at the same moment from the same point in the same direction. The first moves with constant velocity u and the second starts from rest with constant acceleralion f . Then
View SolutionA particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
View Solution

