Question

Establish the following inequalities geometrically or otherwise ,
$\left(a\right)$ | vec A + vec B| -lt | vec A | + |vec B|$,<br>$ | vec A + vec B| gt- ||vec A- | vec B||$<br>\left(C\right)$ | vec A- vec B| -lt | vec A| + vec B|$<br>\left(d\right)|\overrightarrow{A}-\overrightarrow{B}|>-|\left|\overrightarrow{A}\right|-|\overrightarrow{B}\mid |$
When does the equality sign above aplly ?

Explanation

Consider two vectors ` vec A` and `vec B` be represented by the sides `vec (OP)` and ` vec (OQ)` of a parallelogram ` OPSQ`. According to parallelogram law fo vector addition , (vec A + vec B) will be represented by ` vec (OS)` as shown in Fig. 2 (NCT). 16.` Thus ` OP = | vec A| , PQ = PS= | vec B| and ` OS= | vec A+ vec B|`
(a) To prove ` | vec A| +| vec B|-lt | vec A |vec B | + | vec B | `
.
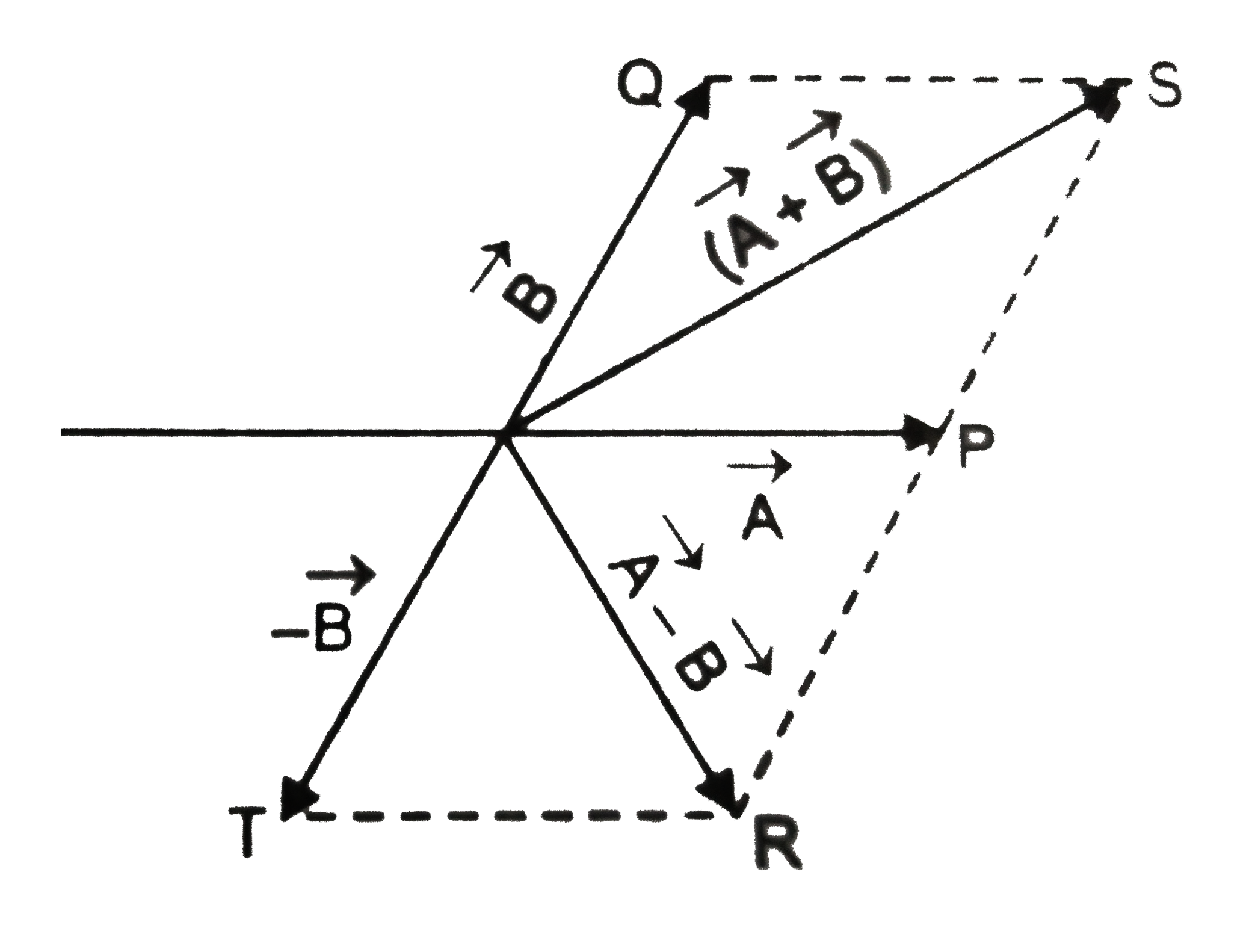We know that length of one side of a triangle is always a triangle is always less than the sun of the longths of the other two sides. Hence from ` Delta OPS`, we have
or` ` | vec A + vec B| lt | vex A |+ |vec A| + | vec B|` ...(i)
If the tqao vectors ` vec A` and vec B` are acting along the same straight line and in the same direction
the ` | vec A + vec B| = | vec A| + | vec B|` ....(ii)
Combining the conditions mentioned in (i) and (ii) we have ` |vec A + vec B | -lt | vec A| + |vec B|`
(b) To prove ` |vec A + vec B| gt- | | vec A | + | vec B||`
For ` Delta OPS`, we have ` OS + PS gt OP ` or ` OS gt OP - PS \ or ` OS gt | OP - OQ |` ...(iii)
(:. PS= OQ)`
The modulus of (OP-PS)` has been taken because the ` L.H.S.` is always positive but the ` R.H.S. may be negative if ` OP lt PS`. Thus frome (iii) we have.
` | vec A + vec B| gt | || vec A|-| vec B||` ...(iv)
If the two vectors ` vec A ` and ` vec B` are acting along a straight line in opposite dirrections. the