If ∣∣→A∣∣=2and∣∣→B∣∣=4, then match the relations in column I with the ange θ between →Aand→B in column II.
Column I, Column II
(a) ∣∣→A×→B∣∣=0 , (i) θ=30∘
(b) ∣∣→A×→B∣∣=0 , (ii) θ=45∘
(c ) →A×→B∣=4 , (iii) θ=90∘
(d) ∣∣→A×x→B∣∣=4√2 , (iv) θ=0∘.
Here A=2andB=4.
(a)∣∣→A×→B∣∣=0=ABsinθ=2×4sinθor=0andθ=0∘. It matches with option (iv).
(b)∣∣→A×→B∣∣=8=ABsinθ2×4sinθorsinθ=1andθ=90∘. It matches with option (iii).
(c)∣∣→A×→B∣∣=4=2×4sinθorsinθ=12orθ=30∘. It matches with option (i).
(d)∣∣→A×→B∣∣=4√2=2×4orsinθ=1√2orθ=45∘. It matches with option (ii).
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 Long answer
Explore 2 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:2 Long answer
Explore 3 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:5 Short answer
Explore 6 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
If ∣∣→A∣∣=2and∣∣→B∣∣=4 , then match the relations in colum I with theange θ between →Aand→B in column II.
Column I , Column II
(a) →A.→B=0 , (i) θ =0<br>(b) vec A . Vec B= + 8,(ii) theta =90^@<br>(c) vec A .vec B =4,(iii) theta =180^@<br>(d) vec A .vec B =- 8,(iv) theta =60^@.
View SolutionGiven below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
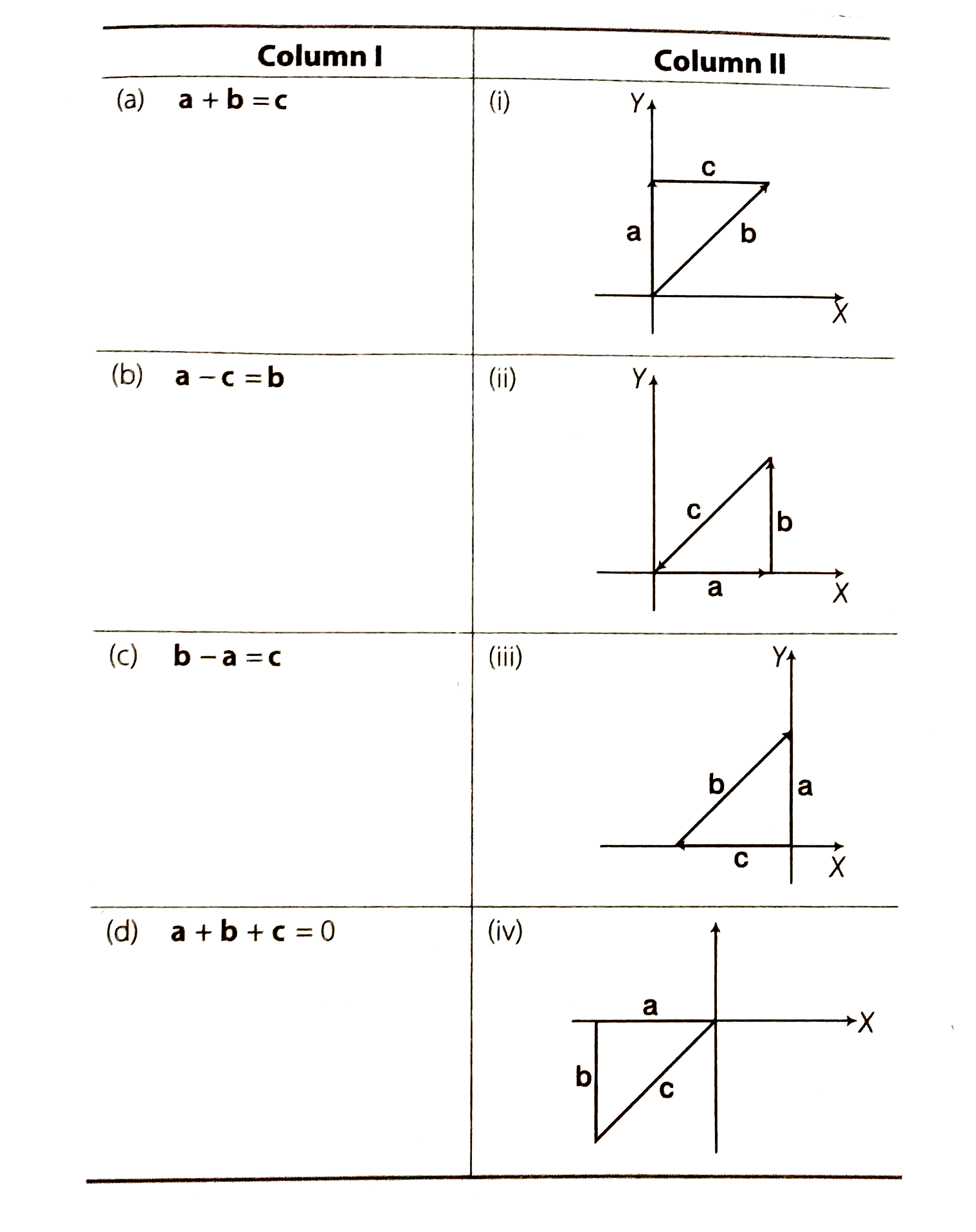
View Solution
Knowledge Check
IF ∣∣→A∣∣=2 and ∣∣→B∣∣=4, then match the relation in Column I with the angle θ between A and B in Column II.

Now, mark the correct above choice from the given codes :Ap-ii, q-i, r-iv,s-iiiBp-iv, q-iii,r-i,s-iiCp-I,q-iii,e-iv,s-iiDp-iii, q-iv, r-i ,s-iiIf →A⋅→B=0and→A×→C=0, then the angle between B and C is
A0B45∘C90∘D60∘If the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
ABA2sinθBBA2cosθCBA2sinθcosθDzero
If ∣∣→A∣∣=2,∣∣→B∣∣=5 and ∣∣→A×→B∣∣=8, din the value of (vec A. vec B0.
View SolutionDefine →ax→b and prove that ∣∣→ax→b∣∣=(→a.→btanθ, where θ is the angle between →a and →b .
View SolutionIf →Aand→B are two vectors satisfying the relation →A⋅→B=∣∣→A×→B∣∣. Then the value of ∣∣→A−→B∣∣ will be :
View SolutionIf →a+→b+→c=0, prove that (→a×→b)=(→b×→c)=(→c×→a)
View Solution.Vectors →A,→B and →c are shown in figure.Find angle between (i) →A and →B. (ii) →A and →C. ,(iii)vec Bandvec C
View Solution

