Question

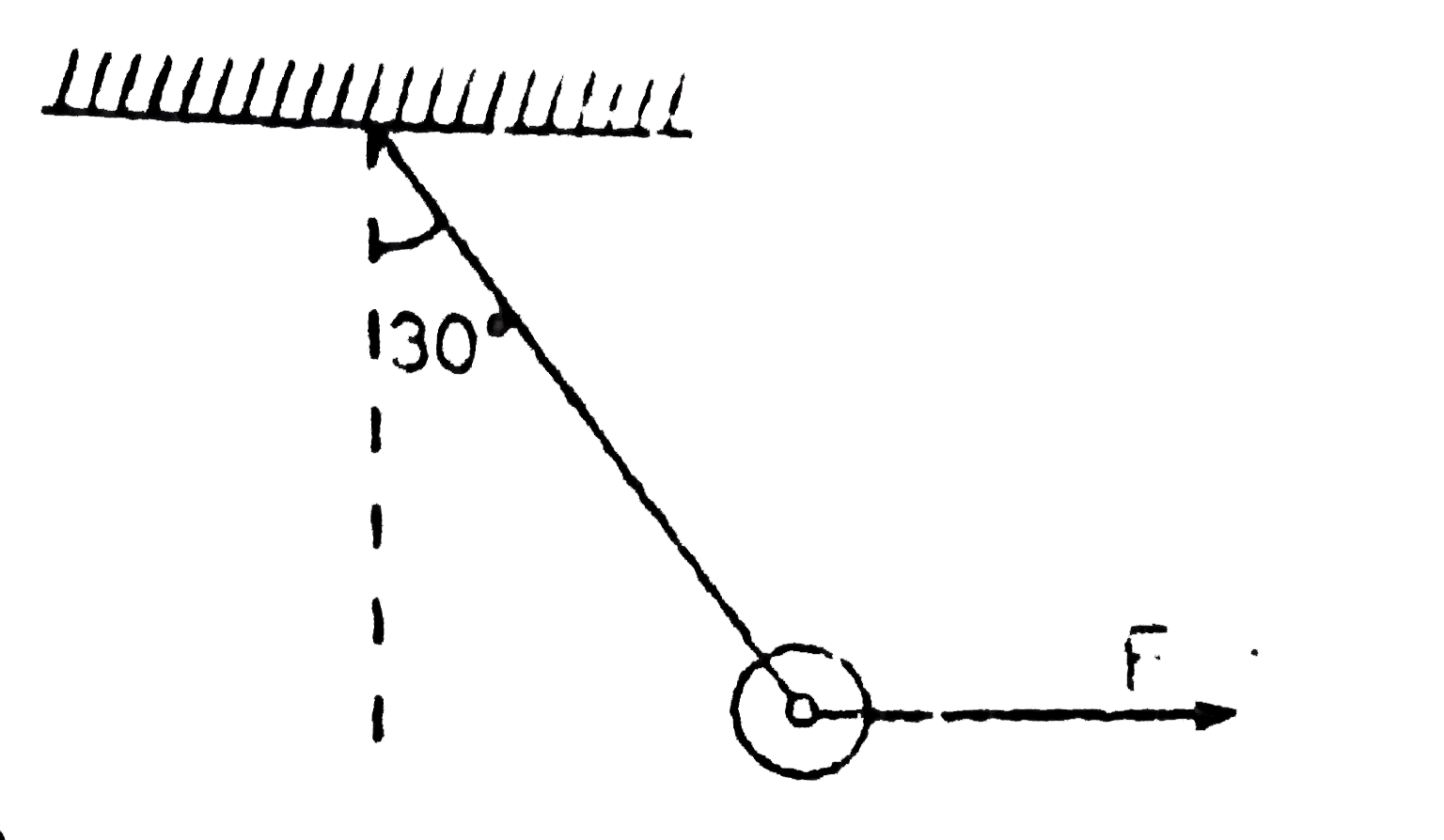
Derermine the horizontal force required to displace a mass of $0.03kg$ suspended by a string until the string makes an angle ${30}^0$ with the vertical.

Explanation

To determine the horizontal force required to displace a mass of 0.03 kg suspended by a string until the string makes an angle of 30 degrees with the vertical, we can follow these steps:

Step 1: Understand the Forces Acting on the Mass
When the mass is displaced, it is in equilibrium under the influence of three forces:
1. The tension (T) in the string.
2. The weight (mg) of the mass acting downwards.
3. The horizontal force (F) acting to displace the mass.

Step 2: Resolve the Tension into Components
The tension in the string can be resolved into two components:
- A vertical component: \( T \cos(30^\circ) \)
- A horizontal component: \( T \sin(30^\circ) \)

Step 3: Apply the Equilibrium Condition
In the vertical direction, the forces must balance:
\( T \cos(30^\circ) = mg \)
Where:
- \( m = 0.03 \, \text{kg} \)
- \( g = 10 \, \text{m/s}^2 \) (approximately)

Step 4: Calculate the Tension (T)
From the equilibrium condition:
\( T = \frac{mg}{\cos(30^\circ)} \)
Substituting the values:
\( T = \frac{0.03 \times 10}{\cos(30^\circ)} \)

Step 5: Calculate \( \cos(30^\circ) \)
We know:
\( \cos(30^\circ) = \frac{\sqrt{3}}{2} \)
Thus, substituting this in:
\( T = \frac{0.03 \times 10}{\frac{\sqrt{3}}{2}} = \frac{0.3}{\frac{\sqrt{3}}{2}} = \frac{0.6}{\sqrt{3}} \)

Step 6: Calculate the Horizontal Force (F)
The horizontal force is given by:
\( F = T \sin(30^\circ) \)
And we know:
\( \sin(30^\circ) = \frac{1}{2} \)
Substituting for T:
\( F = \left(\frac{0.6}{\sqrt{3}}\right) \times \frac{1}{2} = \frac{0.6}{2\sqrt{3}} = \frac{0.3}{\sqrt{3}} \)

Step 7: Simplify the Expression
To express F in numerical form:
\( F = \frac{0.3}{\sqrt{3}} \)
Using \( \sqrt{3} \approx 1.732 \):
\( F \approx \frac{0.3}{1.732} \approx 0.173 \, \text{N} \)

Final Answer
Thus, the horizontal force required to displace the mass is approximately:
\( F \approx 0.173 \, \text{N} \)

---