To find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
The correct Answer is:3
Let a, b, and c be the dimensions of ρ,Sandf to represent d. So,
d=kρaSbfc…..(i)
where k is a dimensionless constant
Writing the dimensions in (i),
M0L1T0=(ML−3)a(MT−3)b(T−1)c
=Ma+bL−3aT−3b−c
Equating the powers of M, L and T, we have
a + b = 0 or a = -b
−3a=1ora=−13orb=+13
From (i) d∝Sbsod∝S1/3
Given d∝S1/n,hencen=3
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Assertion Reason Type Questions
Explore 11 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Comprehension 2.
Explore 4 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:multiple choice Questions
Explore 13 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
Similar Questions
To find the distance d over which a signal can be seen clearly in foggy conditions, a railways engineer uses dimensional analysis and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. The engineer finds that d is proportional to S1/n. The value of n is.
View SolutionA satellite S1 of mass m is revolving at a distance of R from centre of earth and the other satellite S2 of mass 4m is revolving at a distance of 4R from the centre of earth. The time periods of revolution of two satellites are in the raito 1 : n. Find the value of n.
View Solution
Knowledge Check
The mass suspended from the stretched string of a sonometer is 4 kg and the linear mass density of string 4×10−3kgm−1 . If the length of the vibrating string is 100 cm , arrange the following steps in a sequential order to find the frequency of the tuning fork used for the experiment .
(A) The fundamental frequency of the vibratinng string is , n = 12l√Tm.
(B) Get the value of length of the string (l) , and linear mass density (m) of the string from the data in the problem .
(C) Calculate the tension in the string using , T = mg .
(D) Substitute the appropriate values in n=12l√Tm and find the value of 'n' .ABCADBABCDCDCBADBADCIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Distance d between S1andS2 is
 A0.2 mmB45μmC20μmDnone of these
A0.2 mmB45μmC20μmDnone of theseIn Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. When the screen is at position (2), its distance from the double slits is nearly
 A30 cmB20 cmC38 cmDnone of these
A30 cmB20 cmC38 cmDnone of these
A point source of light, S is placed at a distance L in front of the centre of plane mirror of width d which is hanging vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror, at a distance 2L as shown below. The distance over which the man can see the image of the light source in the mirror is nd then value of n is :
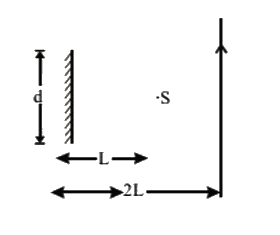
View Solution_E01_101_Q01.png)
Two slits S1 and S2 on the x-axis and symmetric with respect to y-axis are illuminated by a parallel monochromatic light beam of wavelength λ. The distance between the slits is d(>>λ). Point M is the mid point of the line S1S2 and this point is considered as the origin. The slits are in horizontal plane. The interference pattern is observed on a horizontal palte (acting as screen) of mass M, Which is attached to one end of a vertical spring of spring constant K. The other end of the spring is fixed to ground At t=0 the plate is at a distance D(>>d) below the plane of slits and the spring is in its natural length. The plate is left from rest from its initial position. Find the x ad y co-ordinates of the nth maxima on the plate as a function of time. Asuume that spring is light andplate always remains horizontal.
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View SolutionA block of mass 3kg is attached with an ideal spring of spring constant 900 N/m. The other end of the spring connected with a rigid wall. A fixed convex mirror of radius of curvature 120 cm is placed at a distance 110 cm from the block and the spring is in its natural length. the spring is extended by 100 cm and released. the speed of the image of block is (15n)ms, when extension in the spring remains 50 cm. Find the value of 'n'.

View Solution[" A solid sphere of radius "R" is charged with "],[" volume charge density "rho=Kr^(n)," where "K" and "n],[" are constants and "r" is the distance from its "],[" centre.If electric field inside the sphere at "],[" distance "r" is proportional to "r^(4)," then find the "],[" value of "n.]
View Solution

