A voltmeter having least count 0.1 V and an ammeter having least count 0.2 A are used to measure the potentail difference across the ends of a wire and current flowing through the wire respectively. If the reading of voltmeter is 4.4 V and reading of ammeter is 2.2 A, then find (i) the resistance of wire with maximum permissible error and (ii) maximum percentage error.
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Voltmeter reading (V) = 4.4 V
- Ammeter reading (I) = 2.2 A
- Least count of voltmeter (ΔV) = 0.1 V
- Least count of ammeter (ΔI) = 0.2 A
Step 2: Calculate the resistance (R)
Using Ohm's Law, we know that:
R=VI
Substituting the values:
R=4.4V2.2A=2Ω
Step 3: Calculate the maximum permissible error in resistance (ΔR)
The formula for the maximum error in resistance is given by:
ΔRR=ΔVV+ΔII
Rearranging gives:
ΔR=R(ΔVV+ΔII)
Now substituting the values:
- ΔV=0.1V
- ΔI=0.2A
Calculating the individual terms:
ΔVV=0.14.4≈0.02273
ΔII=0.22.2≈0.09091
Now, substituting these into the error formula:
ΔR=2(0.02273+0.09091)
ΔR=2×0.11364≈0.22727Ω
Step 4: Round ΔR to appropriate significant figures
Since we are dealing with measurements, we round ΔR to one decimal place:
ΔR≈0.2Ω
Step 5: Calculate the maximum percentage error
The maximum percentage error is given by:
Percentage Error=(ΔRR)×100
Substituting the values:
Percentage Error=(0.227272)×100≈11.36%
Step 6: Round the percentage error to appropriate significant figures
Rounding to one decimal place gives:
Percentage Error≈11.4%
Final Results
(i) The resistance of the wire with maximum permissible error is:
R=2Ω±0.2Ω
(ii) The maximum percentage error is:
Percentage Error=11.4%
- Voltmeter reading (V) = 4.4 V
- Ammeter reading (I) = 2.2 A
- Least count of voltmeter (ΔV) = 0.1 V
- Least count of ammeter (ΔI) = 0.2 A
Using Ohm's Law, we know that:
R=VI
Substituting the values:
R=4.4V2.2A=2Ω
The formula for the maximum error in resistance is given by:
ΔRR=ΔVV+ΔII
Rearranging gives:
ΔR=R(ΔVV+ΔII)
- ΔV=0.1V
- ΔI=0.2A
ΔVV=0.14.4≈0.02273
ΔII=0.22.2≈0.09091
ΔR=2(0.02273+0.09091)
ΔR=2×0.11364≈0.22727Ω
Since we are dealing with measurements, we round ΔR to one decimal place:
ΔR≈0.2Ω
The maximum percentage error is given by:
Percentage Error=(ΔRR)×100
Substituting the values:
Percentage Error=(0.227272)×100≈11.36%
Rounding to one decimal place gives:
Percentage Error≈11.4%
(i) The resistance of the wire with maximum permissible error is:
R=2Ω±0.2Ω
Percentage Error=11.4%
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Value Based Questions
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Problems for Practice
Explore 130 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Curiosity Questions
Explore 7 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:multiple choice Questions
Explore 13 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
Similar Questions
The voltage across a lamp is (6.0±0.1)V and the current flowing through it is (4.0±0.2)A. Find the power consumed with maximum permissible error in it.
View SolutionThe current flowing through a conductor and the potential difference across its two ends are as per reading of the ammeter and the voltmeter shown in (Fig. 3.50). Find the resistance of the conductor.
 .
.
View Solution
Knowledge Check
A voltmeter has a least count of 0.1 V and an ammeter has a least count of 0.1 A. The potential drop V across a resistance is measured as 10.0 V and current through it is measured as 1.0 A .Select the correct alternative
AThe value of R is (1.0±0.1)×101ΩBThe relative error in measurement of current is 110CThe accuracy in measurement of potential drop is 1100DThe value of R is (10+0.2)Ω
If the voltmeter reads 0.2 V and the ammeter reads 0.101A, the resistance of the voltmeter is (in ohm)A500B1000C200D400If resistance of voltmeter is 10000Ω and resistance of ammeter is 2Ω then find R when voltmeter reads 12 V and ammeter reads 0.1 A
A118ΩB120ΩC124ΩD114Ω
In the circuit shown, voltmeter is ideal and its least count is 0.1 V. The least count of ammeter is 1 mA. Let reading of the voltmeter be 30.0V and the reading of ammeter is 0.020A. Calculate the value of resistance R within error limits.
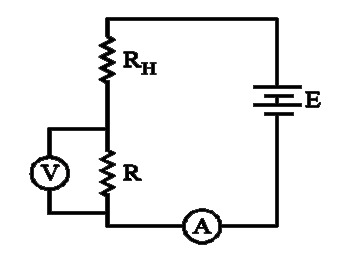
View SolutionA voltmeter of resistance 995Ω is connected across a cell of emf 3V and internal resistance 5Ω. Find the potential difference across the voltmeter, that across the terminals of the cell and percentage error in the reading of voltmeter.
View SolutionThe potential difference across the ends of a wire is found to be (100±2) volt and the current flowing in the wire is found to be (10±0.1)A. What is the maximum percentage error in the measurement of resistance?
View SolutionThe potential difference across the ends of a wire is found to be (100±2) volt and the current flowing in the wire is found to be (10±0.1)A. What is the maximum percentage error in the measurement of resistance?
View SolutionIf resistance of voltmeter is 10000Ω and resistance of ammeter is 2Ω then find R when voltmeter reads 12 V and ammeter reads 0.1 A
View Solution

