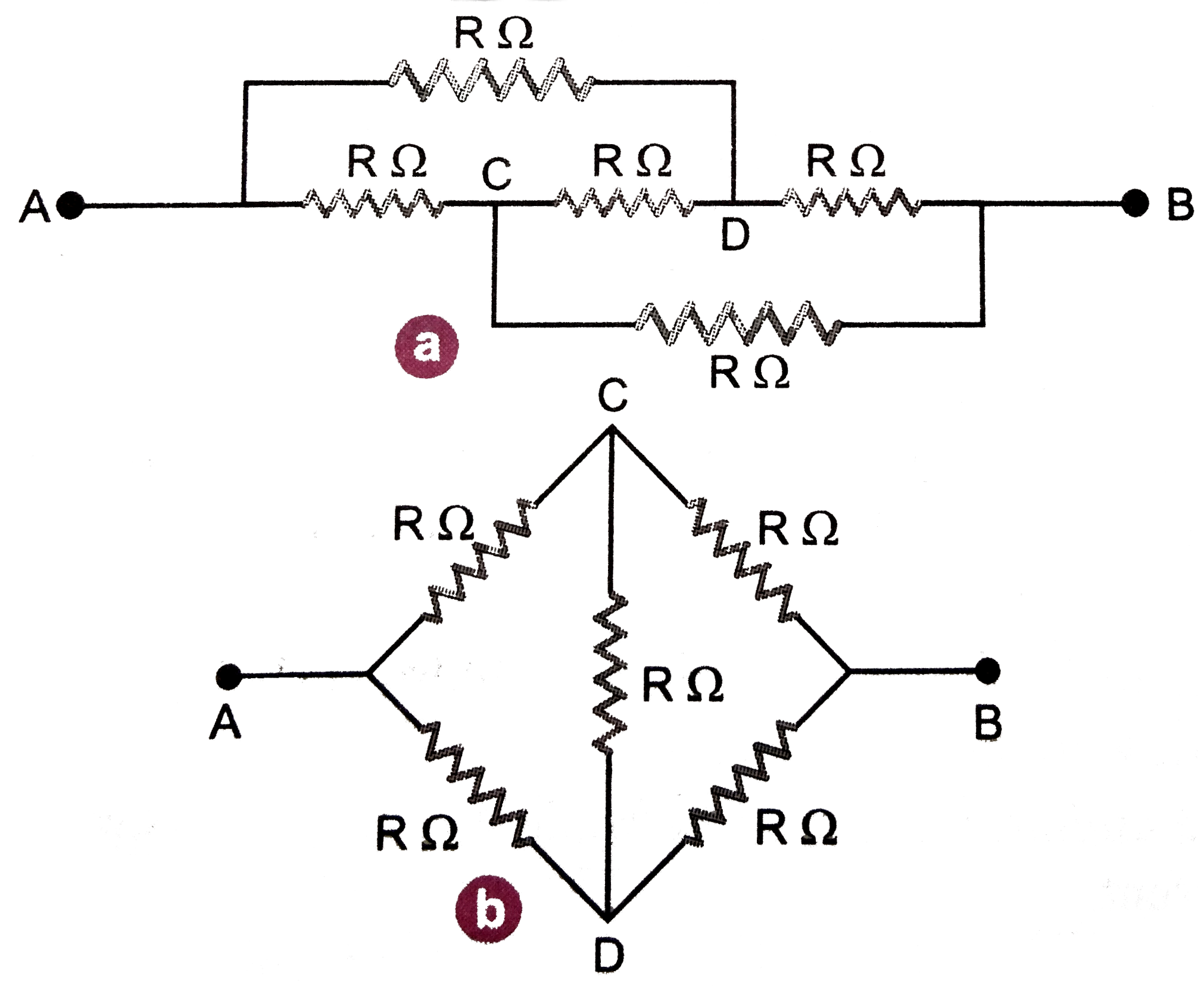
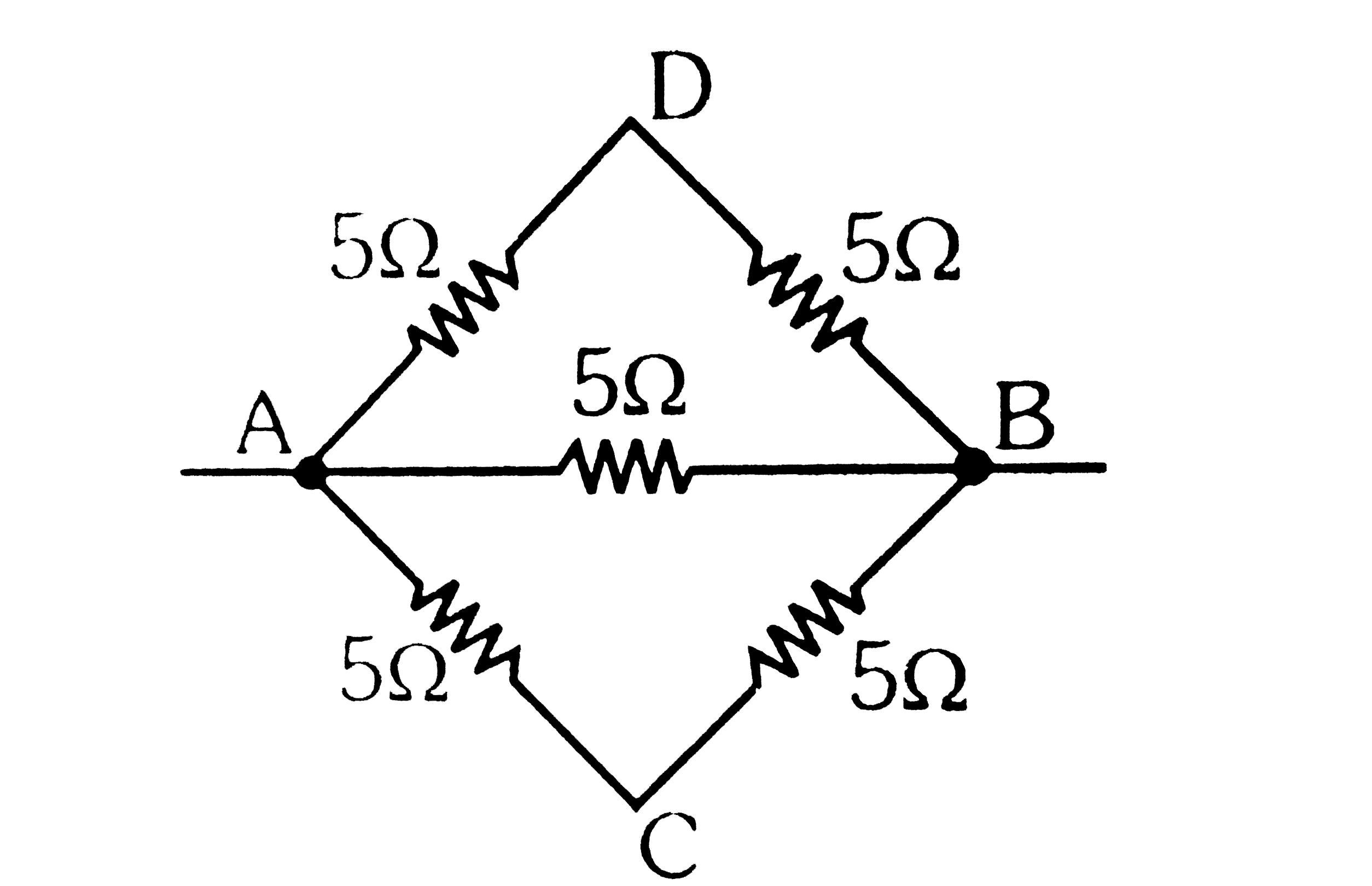
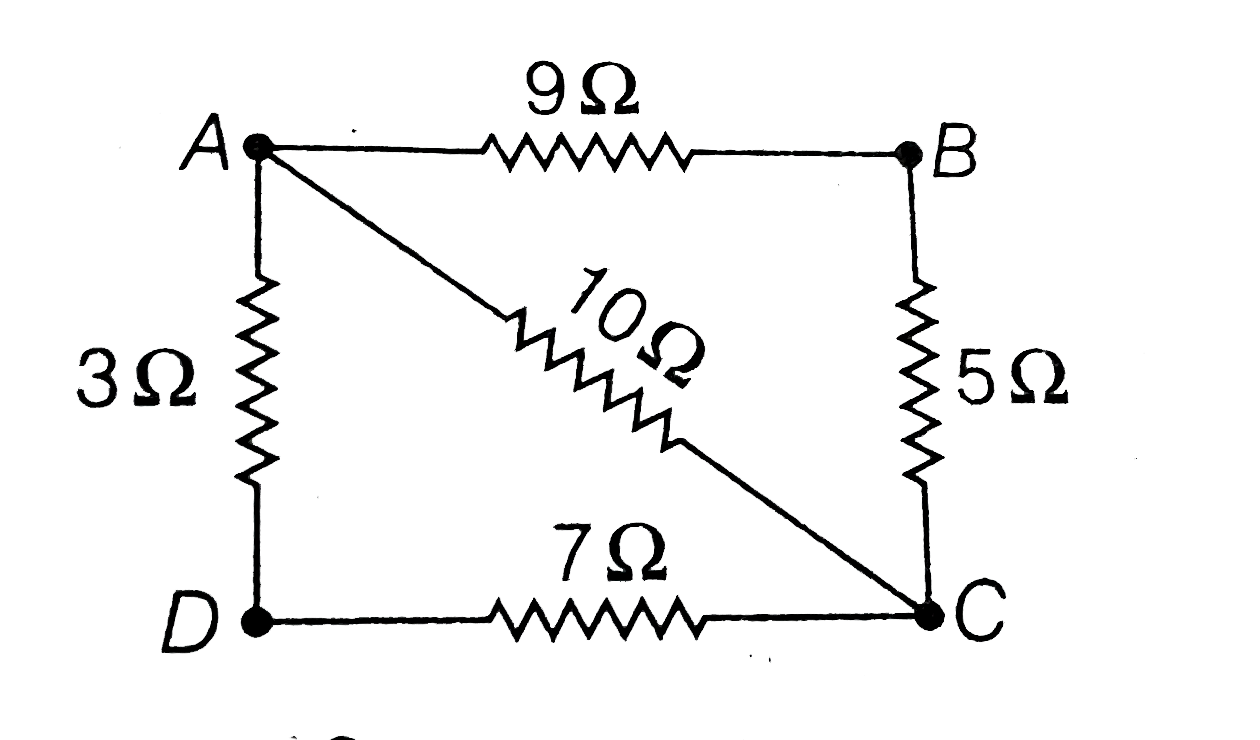
Five resistors, each , are connected as shown in (fig. 3.23). Calculate the resistance between the points
(a) A and b
between the point .
 .
.
Video Solution
Text Solution
The correct Answer is:(a)
(b) .
(i) In (Fig. 3.23), resistance in the arm , i.e.,
As (in arm AB) are in parallel, effective resistance between the points , i.e.,
(ii) Since the effective resistance between points and in the arm and arm are in series, effective resistance between the points .
|
Topper's Solved these Questions
- ELECTRICITYBook:PRADEEPChapter:ELECTRICITYExercise:(Exemplar)Multiple Choice
Explore 18 Videos
- ELECTRICITYBook:PRADEEPChapter:ELECTRICITYExercise:(Mock Test)Sec -A
Explore 21 Videos
- ELECTRICITYBook:PRADEEPChapter:ELECTRICITYExercise:Value Based Question
Explore 4 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBook:PRADEEPChapter:MAGNETIC EFFECTS OF ELECTRIC CURRENTExercise:Mock Test
Explore 21 Videos
Similar Questions
Knowledge Check
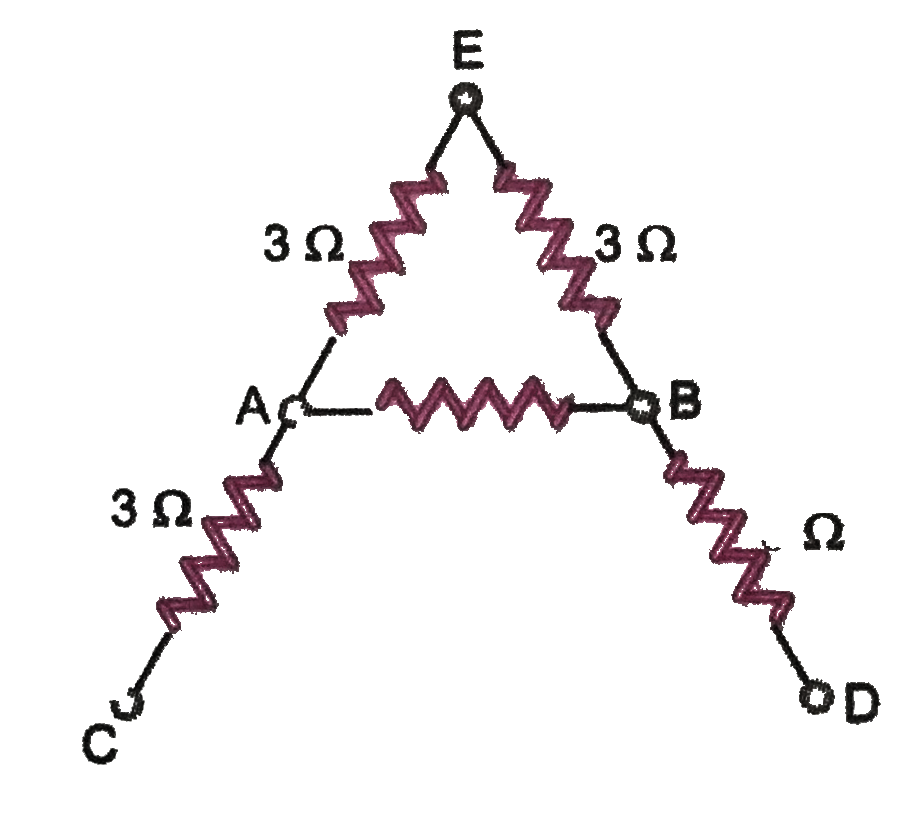
Three resistances each of 3Ω are connected as shown in fig. the resultant resistance between A and F isA9ΩB2ΩC4ΩD1ΩFive resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5ΩFive resistances are connected as shown in the figure. The effective resistance between the points A and B is
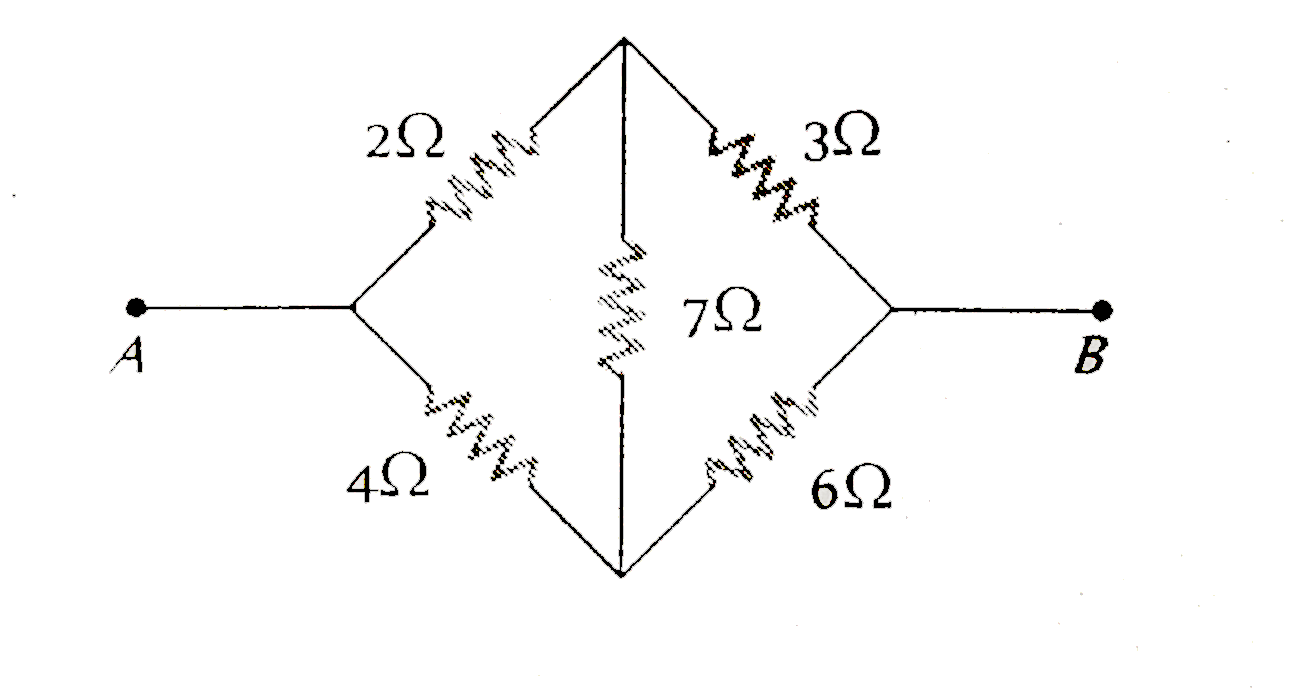 A103ΩB203ΩC15ΩD6Ω
A103ΩB203ΩC15ΩD6Ω
Five resistance are connected as shown in fig. The effective resistancebetween the points A and B is
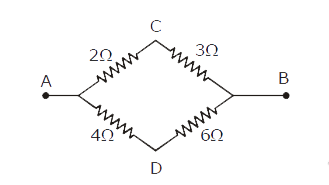
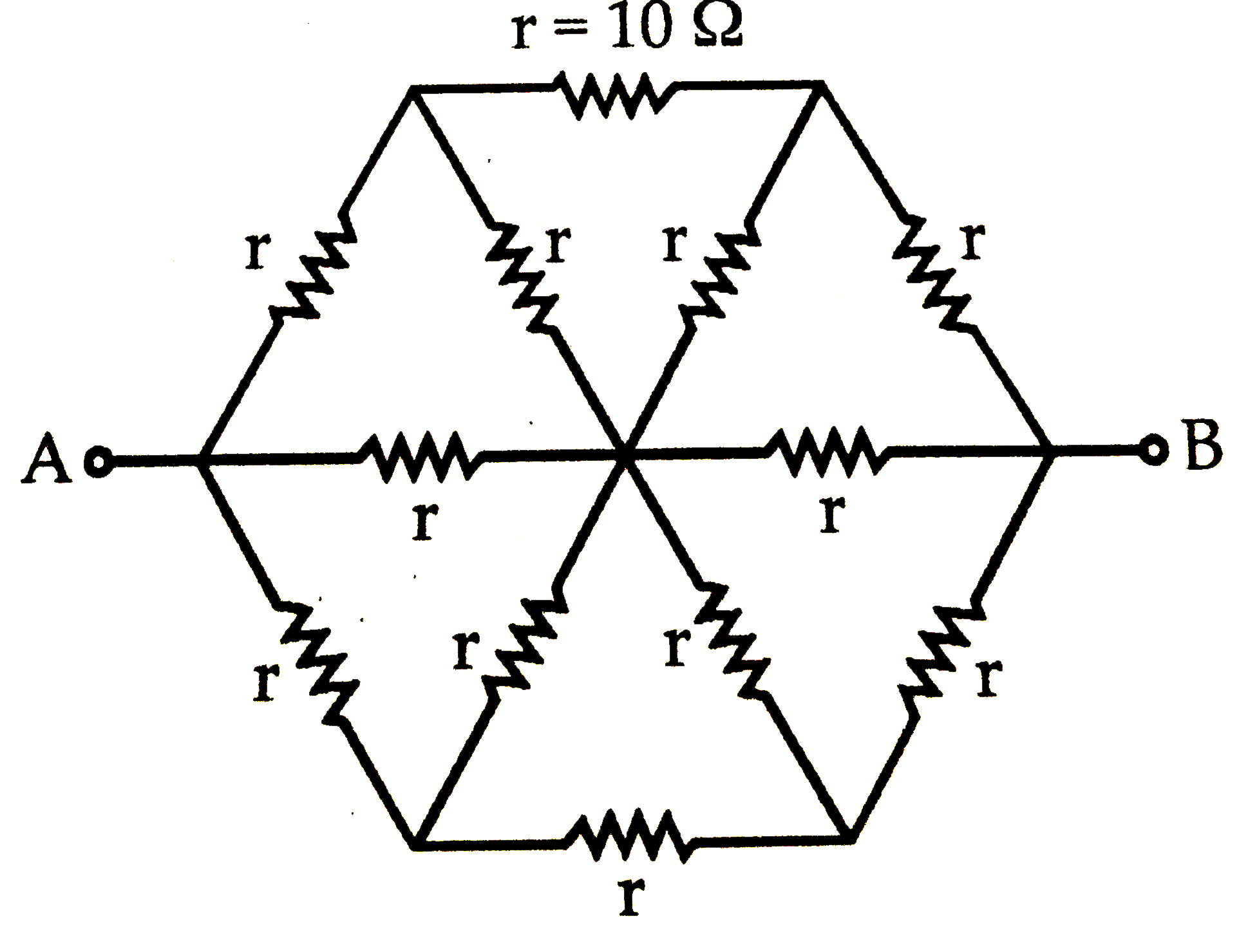
View SolutionIdnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
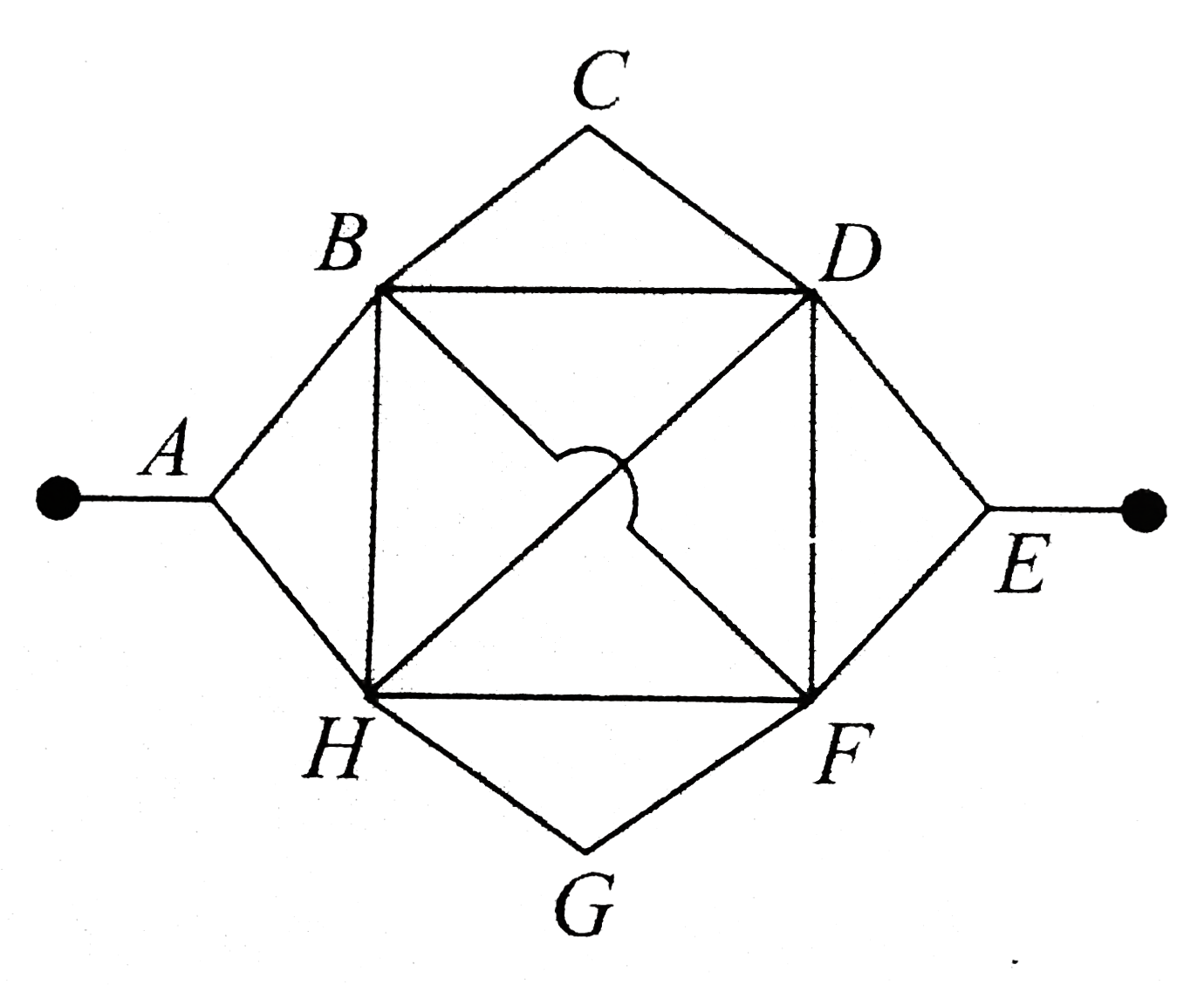
View SolutionFive resistors are connected as shown in figure. Find the equivalent resistance between the points B and C.
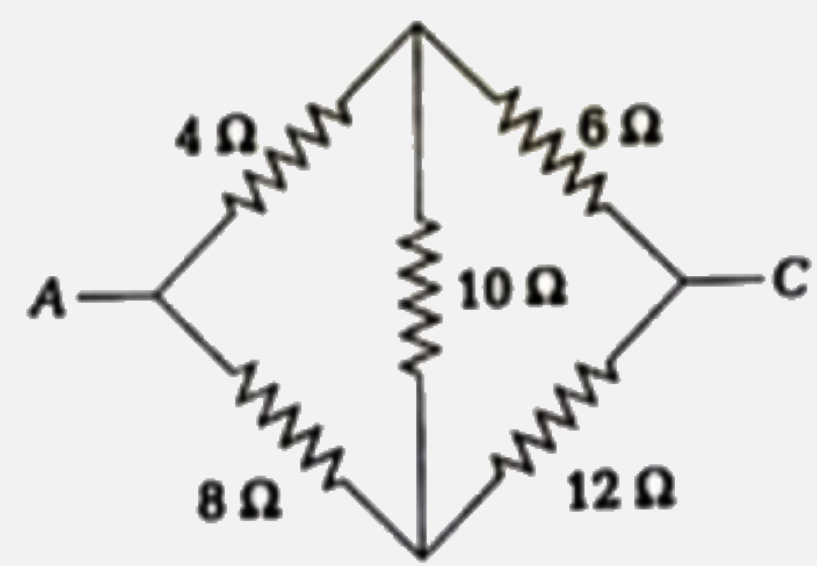
View SolutionFive resistance are connected as shown in the figure. The equivalent resistance between points A and C is
View Solution
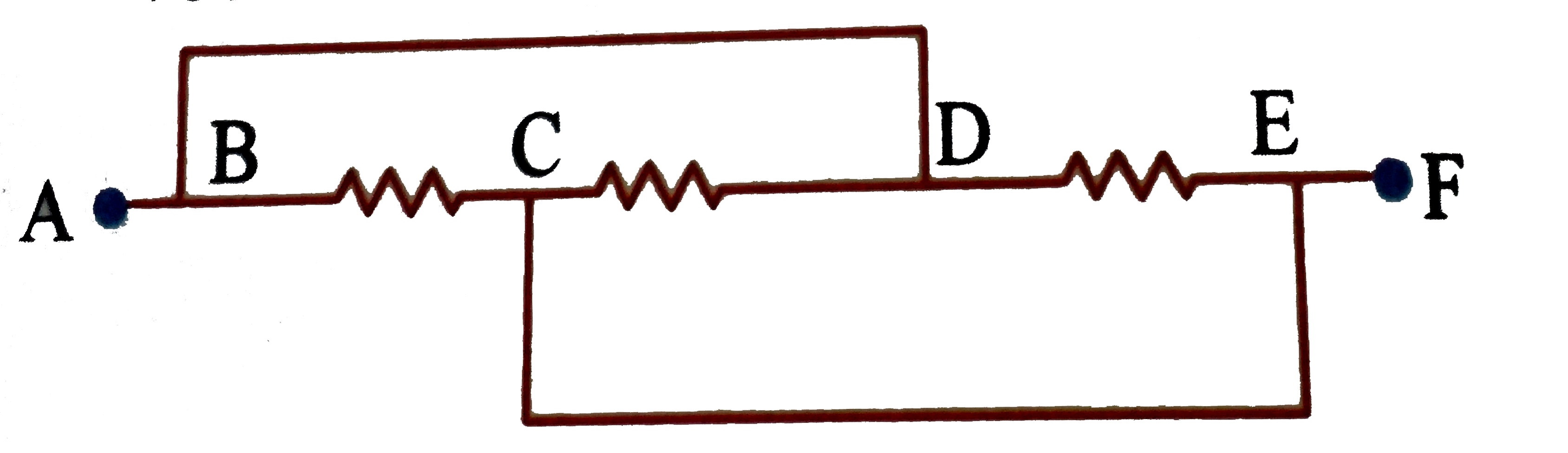
Resistance of each 10Ω are connected as shown in the fig. The effective resistance between A and G is
View Solution