A stone is dropped from the top of a tower 200 m high. At the same time, another stone is projected vertically upwards from the ground with a velocity of 40m/s. Calcuate when and where the two stones will mest.
To solve the problem of when and where the two stones will meet, we can use the equations of motion. Let's break down the solution step by step.
Step 1: Understand the problem
We have two stones:
1. Stone A is dropped from the top of a tower that is 200 m high.
2. Stone B is projected upwards from the ground with an initial velocity of 40 m/s.
We need to find the time t when they meet and the height h at which they meet.
Step 2: Write the equations of motion for both stones
For Stone A (dropped from the tower):
- Initial velocity uA=0 m/s (since it is dropped)
- Distance fallen after time t:
sA=uAt+12gt2=0+12gt2=12gt2
- The height at which Stone A is when they meet is:
hA=200−sA=200−12gt2
For Stone B (projected upwards):
- Initial velocity uB=40 m/s
- Distance traveled upwards after time t:
sB=uBt−12gt2=40t−12gt2
- The height at which Stone B is when they meet is:
hB=sB=40t−12gt2
Step 3: Set the heights equal to find when they meet
Since both stones meet at the same height:
200−12gt2=40t−12gt2
Step 4: Simplify the equation
From the above equation, we can cancel 12gt2 from both sides:
200=40t
Step 5: Solve for time t
t=20040=5 seconds
Step 6: Find the height at which they meet
Now, substitute t=5 seconds back into the equation for either stone to find the height h.
Using Stone A's equation:
hA=200−12gt2
Assuming g≈9.8m/s2:
hA=200−12×9.8×(5)2
hA=200−12×9.8×25
hA=200−122.5=77.5 meters
Conclusion
The two stones will meet after 5 seconds at a height of 77.5 meters from the ground.
---
We have two stones:
1. Stone A is dropped from the top of a tower that is 200 m high.
2. Stone B is projected upwards from the ground with an initial velocity of 40 m/s.
- Initial velocity uA=0 m/s (since it is dropped)
- Distance fallen after time t:
sA=uAt+12gt2=0+12gt2=12gt2
- The height at which Stone A is when they meet is:
hA=200−sA=200−12gt2
- Initial velocity uB=40 m/s
- Distance traveled upwards after time t:
sB=uBt−12gt2=40t−12gt2
- The height at which Stone B is when they meet is:
hB=sB=40t−12gt2
Since both stones meet at the same height:
200−12gt2=40t−12gt2
From the above equation, we can cancel 12gt2 from both sides:
200=40t
t=20040=5 seconds
Now, substitute t=5 seconds back into the equation for either stone to find the height h.
hA=200−12gt2
Assuming g≈9.8m/s2:
hA=200−12×9.8×(5)2
hA=200−12×9.8×25
hA=200−122.5=77.5 meters
The two stones will meet after 5 seconds at a height of 77.5 meters from the ground.
Topper's Solved these Questions
- GRAVITATIONBook:PRADEEPChapter:GRAVITATIONExercise:Worksheet 2
Explore 3 Videos
- GRAVITATIONBook:PRADEEPChapter:GRAVITATIONExercise:Worksheet
Explore 4 Videos
- GRAVITATIONBook:PRADEEPChapter:GRAVITATIONExercise:Quiz testing
Explore 10 Videos
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:MOCK TEST
Explore 36 Videos
- MOTIONBook:PRADEEPChapter:MOTIONExercise:Mock test
Explore 24 Videos
Similar Questions
A stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25ms.Calculate when and where the two stones will meet.
View SolutionA stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stone will meet.
View Solution
Knowledge Check
A stone is dropped from the top of a 400m high tower. At the same time another stone is projected vertically upwards from the ground with a speed of 50m/s. The two stones will cross each other after a time
A2 sB4 sC6 sD8 sOne stone is dropped from a tower from rest and simultaneously another stone is projected vertically upwards from the tower with some initial velocity. The graph of distance (s) between the two stones varies with time (t) as (before either stone hits the ground).
A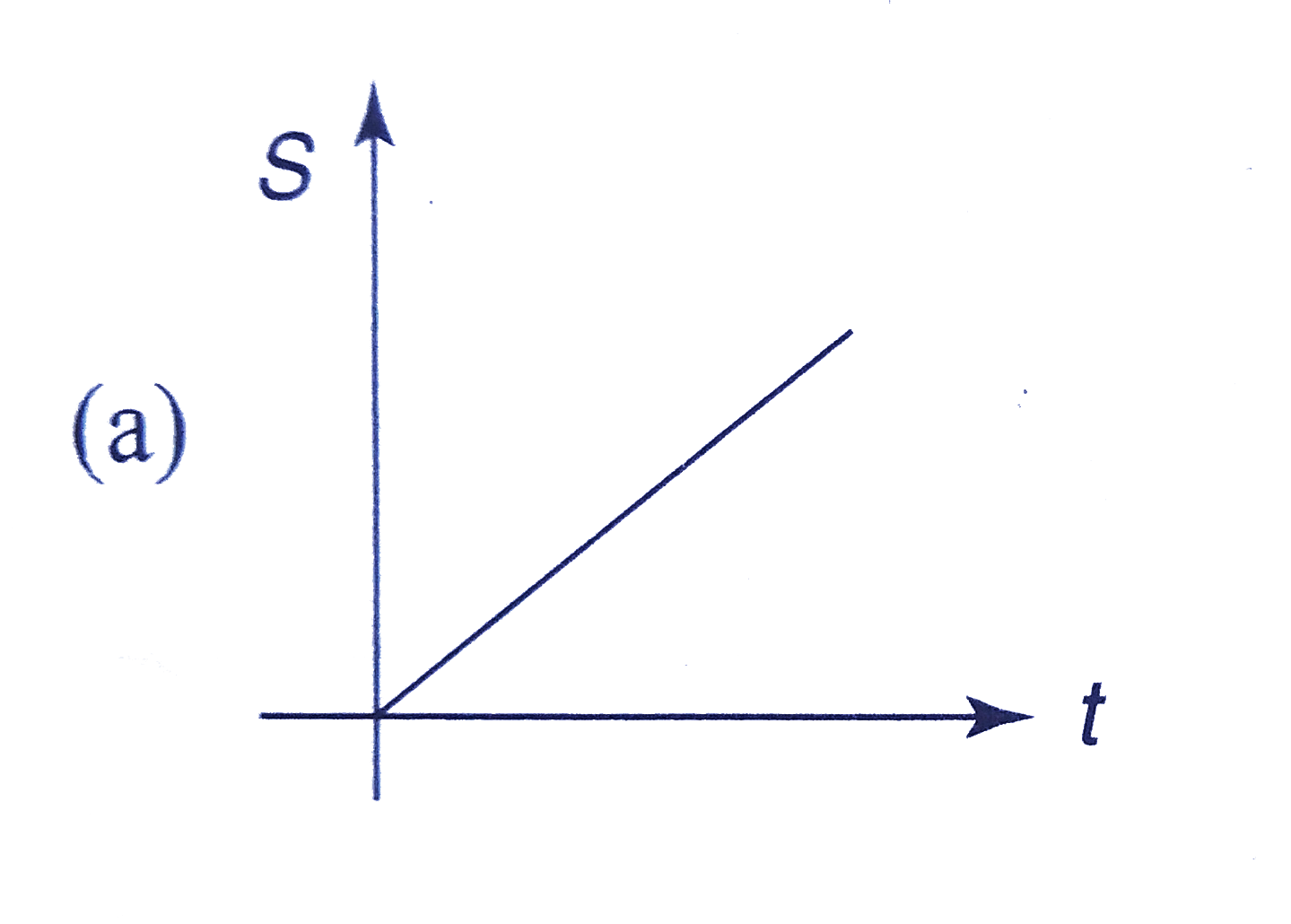 .B
.B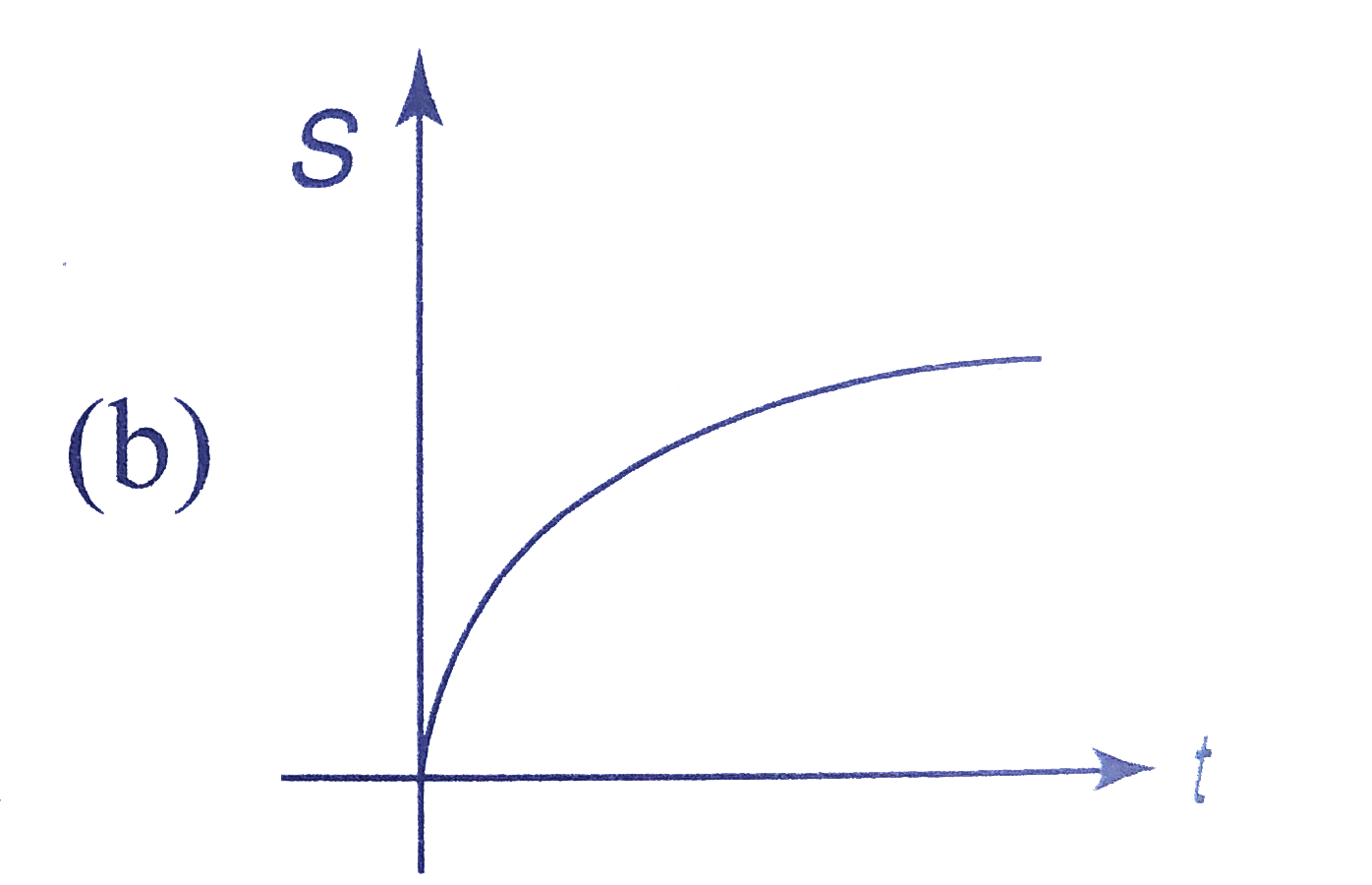 .C
.C .D
.D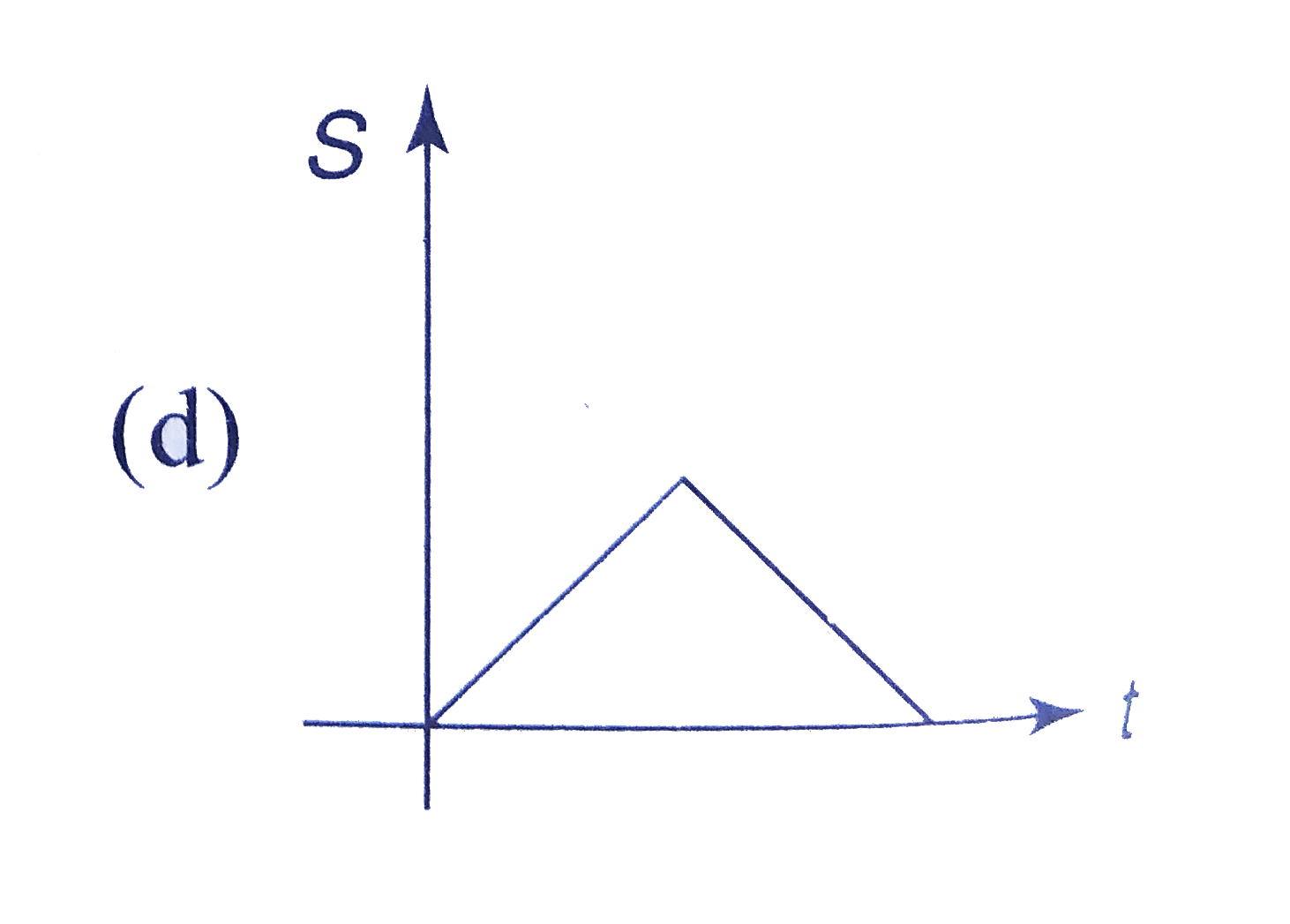 .
.A stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
A18.6 mB39.2 mC44.1 mD98 m

A stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100m/s. Find when and where the two stones meet?
View SolutionFrom the top of a tower 100 m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velocity of 25 m/s. Find when and where the two balls will meet? (g=9.8m/s)
View SolutionForm the top of a tower 100m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velcoity of 25ms−1. Find when and where the two balls will meet.
View SolutionA ball A is dropped from the top of a tower 500m high and at the same instant another ball b is projected upwards with the velocity of 100m/s. after how much time and where the two balls will meet?
View SolutionA stone is dropped from a height of 100m .At the same instant another stone is projected vertically upwards with velocity of 50ms^(-1) .If g=10ms^(-2) ,the height from the ground at which the 2 stones meet is
View Solution

