In Fig. the line that join a planet to the sun sweep out areas A1,A2,A3 in time intervals 6 weeks, 3 weeks and 2 weeks respectively. How are A1,A2,A3 ?realted
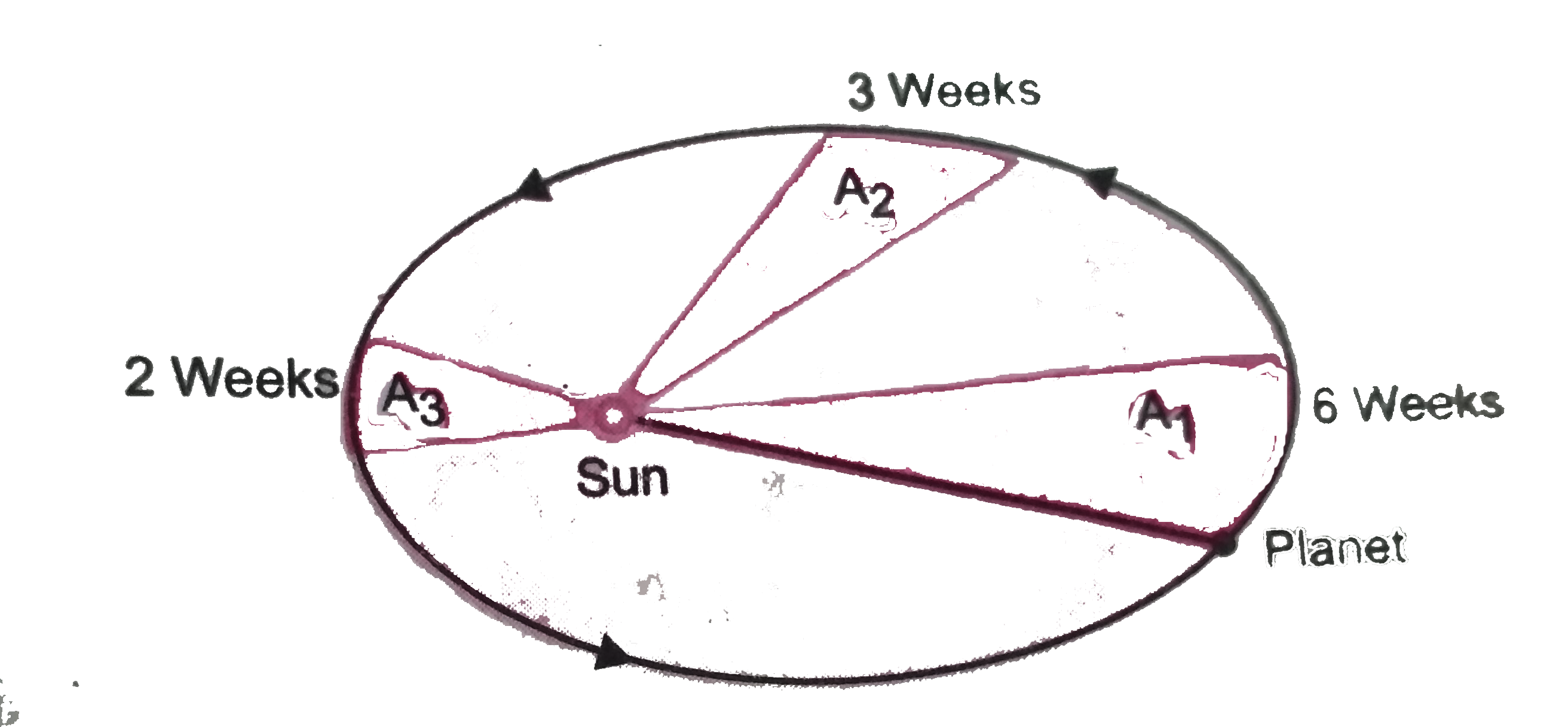
According to Kepler's 2nd law, areal velocity of planet is constant.
∴A16=A23=A32orA1=2A2=3A3
Topper's Solved these Questions
- GRAVITATIONBOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Value Based Questions
4 Videos
- GRAVITATIONBOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Problem for practice
27 Videos
- GRAVITATIONBOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - very short answer
22 Videos
- FORCES AND LAWS OF MOTIONBOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MOCK TEST
36 Videos
- MOTIONBOOK - PRADEEPCHAPTER - MOTIONEXERCISE - Mock test
24 Videos
Similar Questions
The line that joins the saturn to the sun sweeps area A1,A2 and A3 in time intervals of 6 weeks, 3 weeks and 2 weeks respectively as shows in the Fig. What is the correct relation between A1,A2 and A3?
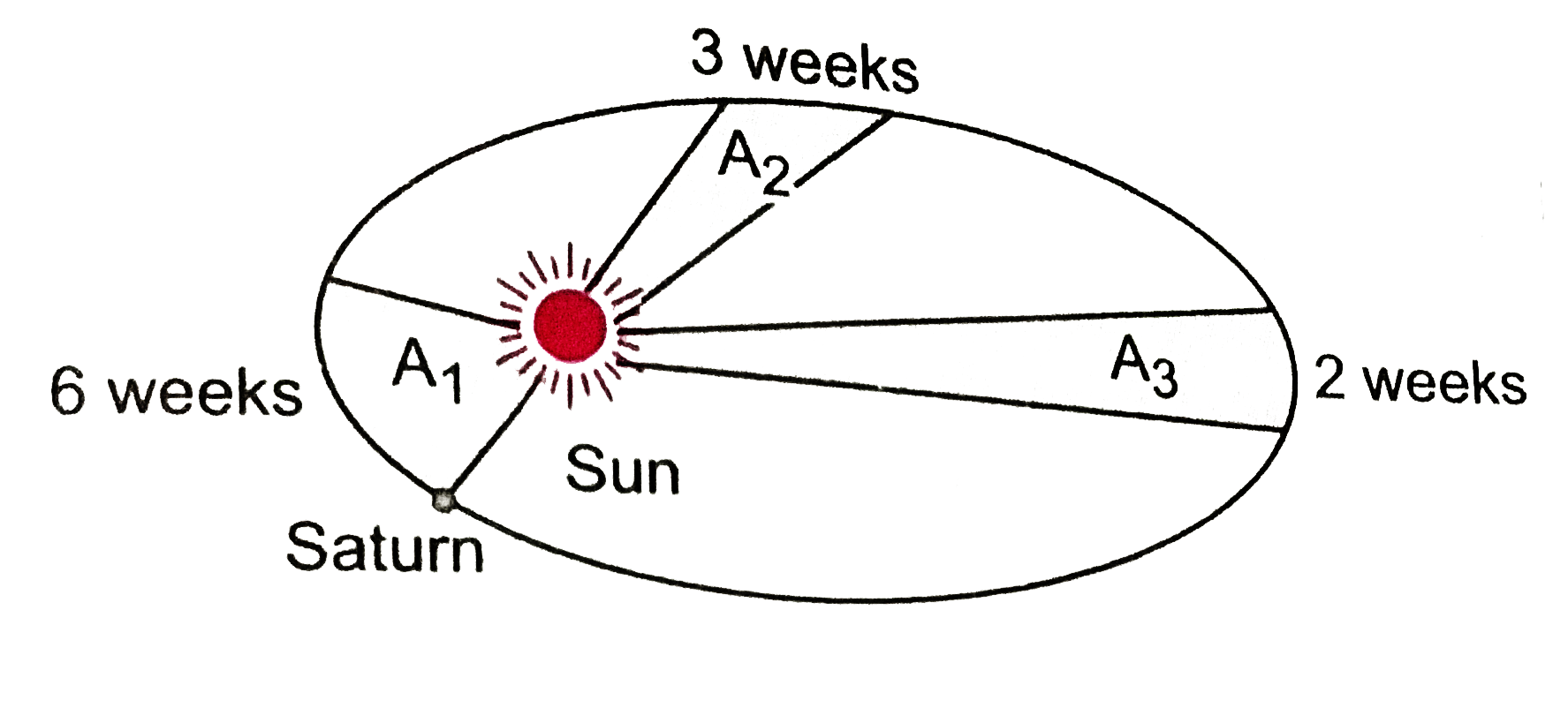
View SolutionThe line that joins the saturn to the sun sweeps area A1,A2 and A3 in time intervals of 6 weeks, 3 weeks and 2 weeks respectively as shows in the Fig. What is the correct relation between A1,A2 and A3?

View Solution
Knowledge Check
A planet moving around the sun sweeps area A1 in 2 days, A2 in 4 days and A3 in 9 days. Then, relation between them
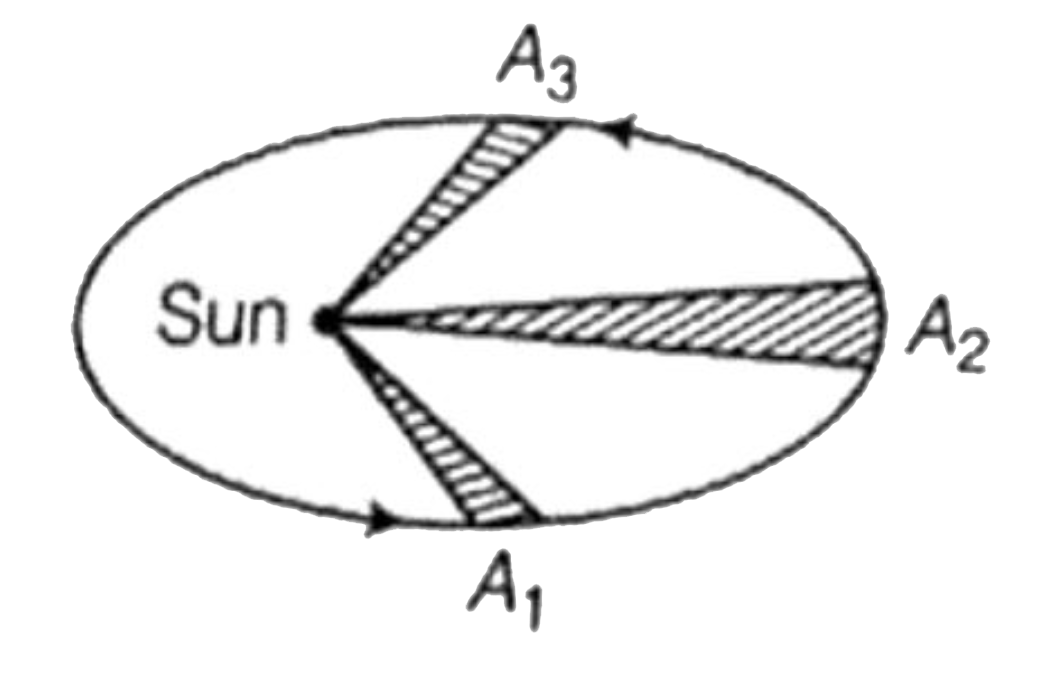 AA1=A2=A3B9A1=3A2=2A3C18A1=9A2=4A3D3A1=4A2=6A3
AA1=A2=A3B9A1=3A2=2A3C18A1=9A2=4A3D3A1=4A2=6A3If A1A2A3A4A5 be regular pentgon inscribed in anunit circle. Then (A1A2)(A1A3) is equal to
A1B3C4D√5Three rectangles A1,A2 and A3 have the same area Their lengths a1,a2 and a3 respectively are such that a1<a2<a3. Cylinders C1,C2 and C3 are formed from A1,A2 and A3 respectively by joining the parallel sides along the breadth. Then,
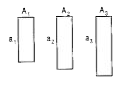 AC1 will enclose maximum volumeBC2 will enclose maximum volumeCC3 will enclose maximum volumeDEach of C1,C2 and C3 will enclose equal volume.
AC1 will enclose maximum volumeBC2 will enclose maximum volumeCC3 will enclose maximum volumeDEach of C1,C2 and C3 will enclose equal volume.
A planet moving around sun sweeps area A1 in 2 days, A2 in 3 days and A3 in 6 days, then find the relation between A1,A2andA3

View SolutionIf a1,a2,a3 are the last three digits of 17256 respectively then the value of a2−a1−a3 is equal
View SolutionIf A1,A2,A3,A4 are four A.M’s between12 and 3, then prove A1+A2+A3+A4 = 7.
View SolutionIf A1,A2,A3,... belongs to AP such that A1+A4+A7+...+A28=140 then maximum value of A1.A2....A28 is
View SolutionIf A1,A2,A3 denote respectively the areas of an inscribed polygon of 2n sides , inscribed polygon of n sides and circumscribed poylgon of n sides ,then A1,A2,A3 are in
View Solution
