A truck of mass M is moved under a force F. If the truck is then loaded with an object equal to the mass of the truck and the driving force is halved, then how does the acceleration change?
To solve the problem, we will analyze the situation using Newton's second law of motion, which states that the force acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma).
1. Identify the Initial Conditions:
- Let the mass of the truck be M.
- The initial force applied to the truck is F.
- According to Newton's second law, the initial acceleration A can be expressed as:
F=M⋅A(Equation 1)
2. Determine the New Conditions After Loading:
- The truck is loaded with an object equal to its mass, so the new mass of the truck becomes 2M.
- The driving force is halved, so the new force is F2.
- We need to find the new acceleration A′ under these new conditions. According to Newton's second law:
F2=2M⋅A′(Equation 2)
3. Set Up the Equations:
- From Equation 1, we can express A:
A=FM
- From Equation 2, we can express A′:
A′=F22M=F4M
4. Relate the Two Accelerations:
- Now, we can relate A′ to A:
A′=F4M=14⋅FM=A4
5. Conclusion:
- Therefore, the new acceleration A′ is one-fourth of the initial acceleration A:
A′=A4
Final Answer:
The acceleration changes to one-fourth of the initial acceleration.
- Let the mass of the truck be M.
- The initial force applied to the truck is F.
- According to Newton's second law, the initial acceleration A can be expressed as:
F=M⋅A(Equation 1)
- The truck is loaded with an object equal to its mass, so the new mass of the truck becomes 2M.
- The driving force is halved, so the new force is F2.
- We need to find the new acceleration A′ under these new conditions. According to Newton's second law:
F2=2M⋅A′(Equation 2)
- From Equation 1, we can express A:
A=FM
- From Equation 2, we can express A′:
A′=F22M=F4M
- Now, we can relate A′ to A:
A′=F4M=14⋅FM=A4
- Therefore, the new acceleration A′ is one-fourth of the initial acceleration A:
A′=A4
The acceleration changes to one-fourth of the initial acceleration.
Topper's Solved these Questions
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:LONG ANSWER QUESTIONS
Explore 10 Videos
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:VERY SHORT ANSWER QUESTIONS
Explore 29 Videos
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:NCERT QUESTIONS
Explore 30 Videos
- FLOTATIONBook:PRADEEPChapter:FLOTATIONExercise:Problem For Practice
Explore 6 Videos
- GRAVITATIONBook:PRADEEPChapter:GRAVITATIONExercise:Model Test paper (1)
Explore 36 Videos
Similar Questions
A block of mass 2kg is placed on a truck as shown in the figure. The coefficient of friction between the block and surface is 0.5. The truck starts from the rest and moves with acceleration a0. (a) Find the friction force acting on the block if (i) a0=2m/s2 , (ii) 4m/s2 , (iii) 6m/s2 and (b) if acceleration of truck a0=8m/s2. After how much time the blocks falls off the truck and the distance travelled by the truck in this time.

View SolutionAn empty truck of mass 1000 kg is moving at a speed of 36 km h−1. It is loaded with 500 kg material on its way and again moves with the same speed. Will the momentum of the truck remain the same after loading? If not, find the momentum of the truck after loaded.
View Solution
Knowledge Check
A block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck
 AThe particle will execute SHMBThe time period of oscillations will be 2π√mk(Cthe amplitude of oscillations will be (m2a20)DThe energy of oscillatioins will be m2a20k
AThe particle will execute SHMBThe time period of oscillations will be 2π√mk(Cthe amplitude of oscillations will be (m2a20)DThe energy of oscillatioins will be m2a20kA moving truck crashes into a stationary car. The truck's mass is ten times that of the car. How does the magnitude of the force exerted by the truck on the car compared with the exerted by the car on the truck
AThe force the truck exerts on the car is ten times bigger.Bthe force that the truck exerts on the car is ten times smallerCThe ratio depends on the speed of the truckDThey are the sameA truck of mass 10 metric ton runs at 3ms−1 along a level track and collides with a loaded truck of mass 20 metric ton, standing at rest. If the trucks couple together , the common speed after the collision is
A1ms−1B0.1ms−1C0.5ms−1D0.3ms−1
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
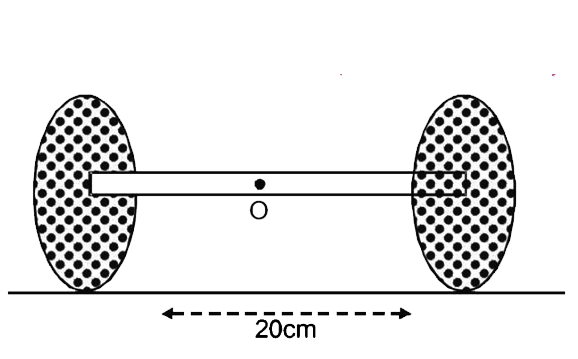
View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
View SolutionA block of mass 1kg is kept on smooth floor of a truck. One end of a spring of force constant 100N/m is attached to the block and other end is attached to the body of truck as shown in the figure. At t=0, truck begins to move with constant acceleration 2m/s2. The amplitude of oscillation of block relative to the floor of truck is
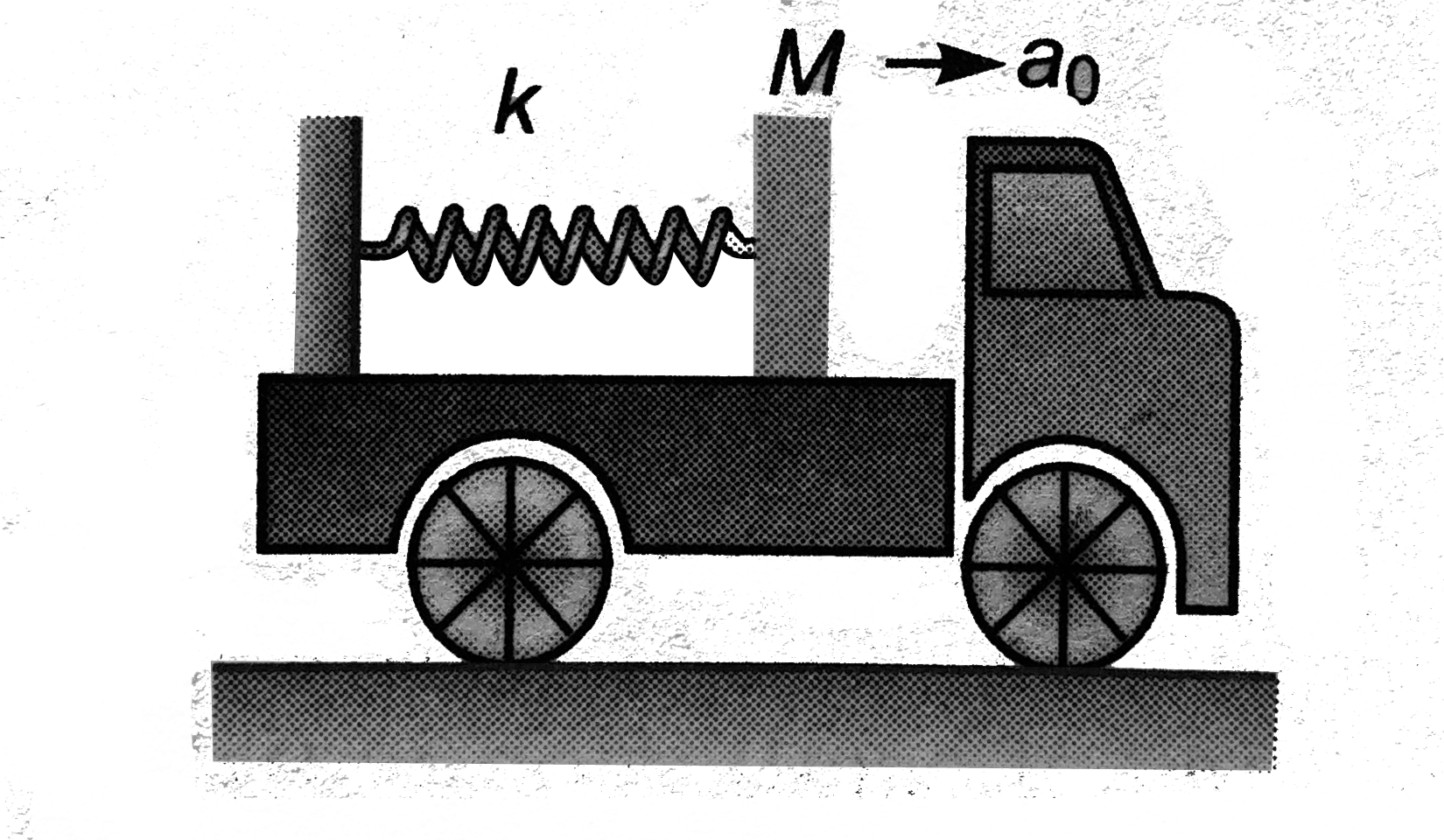
View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in the figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truj starts moving towards right with a constant acceleration a0. If the block is observed from the truck

View SolutionA man tries hard to push a loaded truck but fails to move it. In tis case he does
View Solution

