A motorcycle is moving with a velocity of and it takes to stop after the brakers are applied. Calculate the force exerted by the brakers on the motorcycle if its mass alongwith the rider is
-100 N
500 N
200 N
-1000 N
The correct Answer is:D
To solve the problem step by step, we will follow these calculations:
Step 1: Convert the velocity from km/h to m/s
The motorcycle is moving at a velocity of 90 km/h. To convert this to meters per second (m/s), we use the conversion factor 518.
Velocity in m/s=90×518=25m/s
Step 2: Identify the initial and final velocities
- Initial velocity (u) = 25 m/s (as calculated above)
- Final velocity (v) = 0 m/s (since the motorcycle comes to a stop)
Step 3: Determine the time taken to stop
The time taken (t) to stop is given as 5 seconds.
Step 4: Use the first equation of motion to find acceleration
We can use the first equation of motion:
v=u+at
Substituting the known values:
0=25+a×5
Rearranging the equation to solve for acceleration (a):
a×5=−25
a=−255=−5m/s2
Step 5: Calculate the force exerted by the brakes
Using Newton's second law of motion, the force (F) can be calculated using the formula:
F=m×a
Where:
- m = mass of the motorcycle and rider = 200 kg
- a = acceleration = -5 m/s²
Substituting the values:
F=200×(−5)=−1000N
Step 6: Interpret the result
The negative sign indicates that the force exerted by the brakes is in the opposite direction to the motion of the motorcycle.
Final Answer
The force exerted by the brakes on the motorcycle is 1000N (opposing the motion).
---
The motorcycle is moving at a velocity of 90 km/h. To convert this to meters per second (m/s), we use the conversion factor 518.
- Initial velocity (u) = 25 m/s (as calculated above)
- Final velocity (v) = 0 m/s (since the motorcycle comes to a stop)
The time taken (t) to stop is given as 5 seconds.
We can use the first equation of motion:
a=−255=−5m/s2
Using Newton's second law of motion, the force (F) can be calculated using the formula:
- m = mass of the motorcycle and rider = 200 kg
- a = acceleration = -5 m/s²
The negative sign indicates that the force exerted by the brakes is in the opposite direction to the motion of the motorcycle.
The force exerted by the brakes on the motorcycle is 1000N (opposing the motion).
Topper's Solved these Questions
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:NCERT QUESTIONS
Explore 30 Videos
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:SHORT ANSWER QUESTIONS
Explore 44 Videos
- FLOTATIONBook:PRADEEPChapter:FLOTATIONExercise:Problem For Practice
Explore 6 Videos
- GRAVITATIONBook:PRADEEPChapter:GRAVITATIONExercise:Model Test paper (1)
Explore 36 Videos
Similar Questions
A motor car is moving with a velocity of 108km/h and it takes 4second to stop after the brakes are applied. Calculate the force exerted by the brakes on the motorcar if its mass along with the passenger is 1000kg.
View SolutionA motor car is moving with a velocity of 108km/h and it takes 4second to stop after the brakes are applied. Calculate the force exerted by the brakes on the motorcar if its mass along with the passenger is 1000kg.
View Solution
Knowledge Check
An 800-kg car is moving at a speed of 90 km/h. it takes 5s to stop after the brakes are applied. The force applied by the brakes will be _______ .
A3000 NB4000 NC1000 ND2000 NA bullet of mass 0.05 kg moving with a speed of 80m/s enters a wooden block and is stopped after a distance of 0.40 m The average resistive force exerted by the block on the bullet is:
A300 NB20 NC400 ND40 N
A body of mass 2kg moving with a velocity of 10m/s is brought to rest in 5sec. Calculate the stopping force applied.
View SolutionA scooter acquires a velocity of 36km/h in 10seconds just after the start . It takes 20 seconds to stop . Calculate the acceleration in the two cases.
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
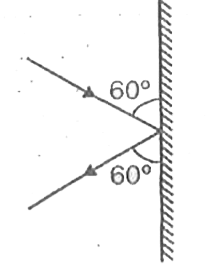
View SolutionA car of mass 2400 kg moving with a velocity of 20 m s−1 is stopped in 10 seconds on applying brakes Calculate the retardation and the retarding force.
View SolutionA body of mass 5 kg is moving with a velocity of 10 m/s. A force is applied to it so that in 25 seconds, it attains a velocity of 35 m/s. Calculate the value of the force applied.
View SolutionA car of mass 800 kg is moving with a constant velocity 40 km/h. Find the net force on it.
View Solution

