The time taken by a particle performing SHM on a straight line to pass from point A to B where its velocities are same is 2 seconds .After another 2 seconds it return to B The time period of oscillation is (in seconds)
2
4
6
8
The correct Answer is:D
To solve the problem, we need to analyze the motion of the particle performing Simple Harmonic Motion (SHM) between points A and B. Given that the time taken to pass from point A to point B, where the velocities are the same, is 2 seconds, and it takes another 2 seconds to return to point B, we can deduce the time period of the oscillation.
1. Understanding the Motion:
- The particle moves from point A to point B in 2 seconds.
- The particle has the same velocity at points A and B, indicating that these points are symmetrically located about the mean position O.
2. Time Taken for One Complete Cycle:
- Since the time taken to go from A to B is 2 seconds, and the particle returns to B after another 2 seconds, the total time taken from A to B and back to B is 2+2=4 seconds.
- However, this only accounts for the motion from A to B and back to B.
3. Completing the Full Oscillation:
- To complete one full oscillation (from A to B, then back to A), we need to consider the time taken to go from B back to A.
- Since the motion is symmetrical, the time taken to go from B to A will also be 2 seconds.
4. Calculating the Total Time Period:
- Therefore, the total time for one complete cycle (from A to B, back to A) is:
Total Time Period=Time from A to B+Time from B to A=2+2+2=6 seconds
5. Final Calculation:
- The total time period of the oscillation is thus 6 seconds.
Conclusion:
The time period of oscillation is 6 seconds.
---
- The particle moves from point A to point B in 2 seconds.
- The particle has the same velocity at points A and B, indicating that these points are symmetrically located about the mean position O.
- Since the time taken to go from A to B is 2 seconds, and the particle returns to B after another 2 seconds, the total time taken from A to B and back to B is 2+2=4 seconds.
- However, this only accounts for the motion from A to B and back to B.
- To complete one full oscillation (from A to B, then back to A), we need to consider the time taken to go from B back to A.
- Since the motion is symmetrical, the time taken to go from B to A will also be 2 seconds.
- Therefore, the total time for one complete cycle (from A to B, back to A) is:
Total Time Period=Time from A to B+Time from B to A=2+2+2=6 seconds
- The total time period of the oscillation is thus 6 seconds.
The time period of oscillation is 6 seconds.
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Velocity , Acceleration And Energy Of Simple Harmonic Motion
40 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Spring Particle System
24 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
The time taken by a particle performing SHM on a straight line to pass from point A to B where its velocities are same is 2 seconds . After another 2 second it returns to B .The time peroid of oscillation is (in seconds):
A2B4C6D8The time taken by a particle performing SHM to pass from point A and B where it is velocities are same is 2:3. After another 2 s it returns to B. The time period oscillation is (in seconds)
A2B8C6D4The time taken by a particle performing SHM to pass from point A to B where its velocities are same is 2s. After another 2s it returns to B. The ratio of distance OB to its a amplitude (where O is the mean position) is
A1:√2B(√2−1):1C1:2D1:2√2
Assertion : A particle performing SHM at certain instant is having velocity v. It again acquire a velocity v for the first time after a time interval of T second. Then the time period of oscillation is T second.
Reason : A particle performing SHM can have same velocity at two instants in one cycle.
View SolutionThe displacement of a particle performing a S.H.M. is given by x=0.5sin100π(t+0.05), where x is in metres and t is in second. Its periodic time in second is
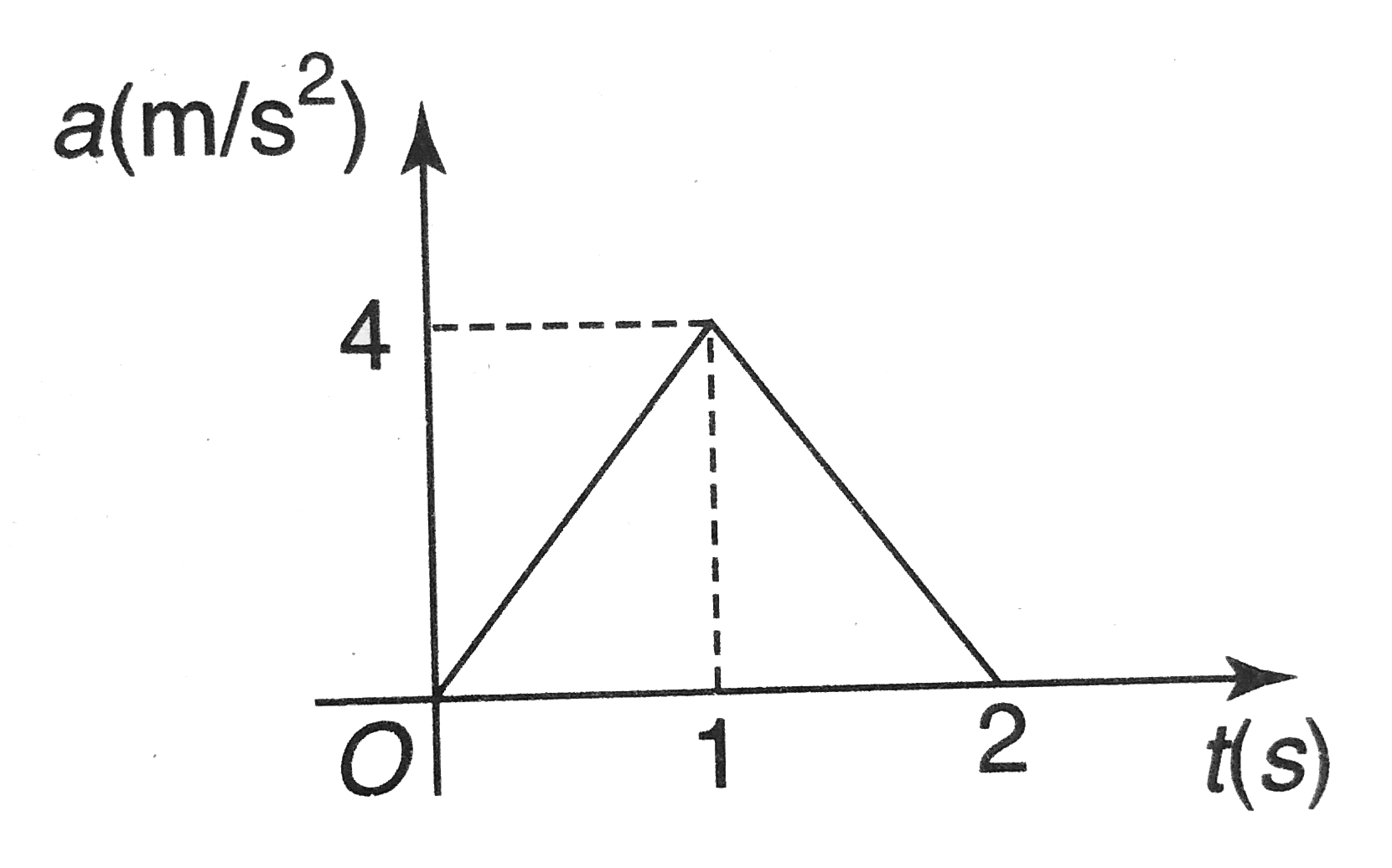
View SolutionThe acceleration-time graph of a particle moving in a straight line is as shown in figure. The velocity of the particle at time t=0 is 2m/s. The velocity after 2 seconds will be
View SolutionThe phase of a particle performing S.H.M. increases by π/2 after every 4 seconds. Its time period of oscillation is
View SolutionA particle performs SHM in a straight line. In the first second, starting from rest, it travels a distance a and in the next second it travels a distance b in the same direction. The amplitude of the SHM is
View Solution