Assertion : The equivalent thermal conductivity of two plates of same thickness in contact (series) is less than the smaller value of thermal conductivity.
Reason : For two plates of equal thickness in contact (series) the equivalent thermal conductivity is given by
1K=1K1+1K2
If both the assertion and reason are true and reason is the correct explanation of the assertion.
If both the assertion and reason are true but the reason is not correct explanation of the assertion.
If the assertion is true but the reason is false
If the both the assertion and reason are false.
The correct Answer is:D
Equivalent thermal conductivity of two equally thick plates in series combination is given by
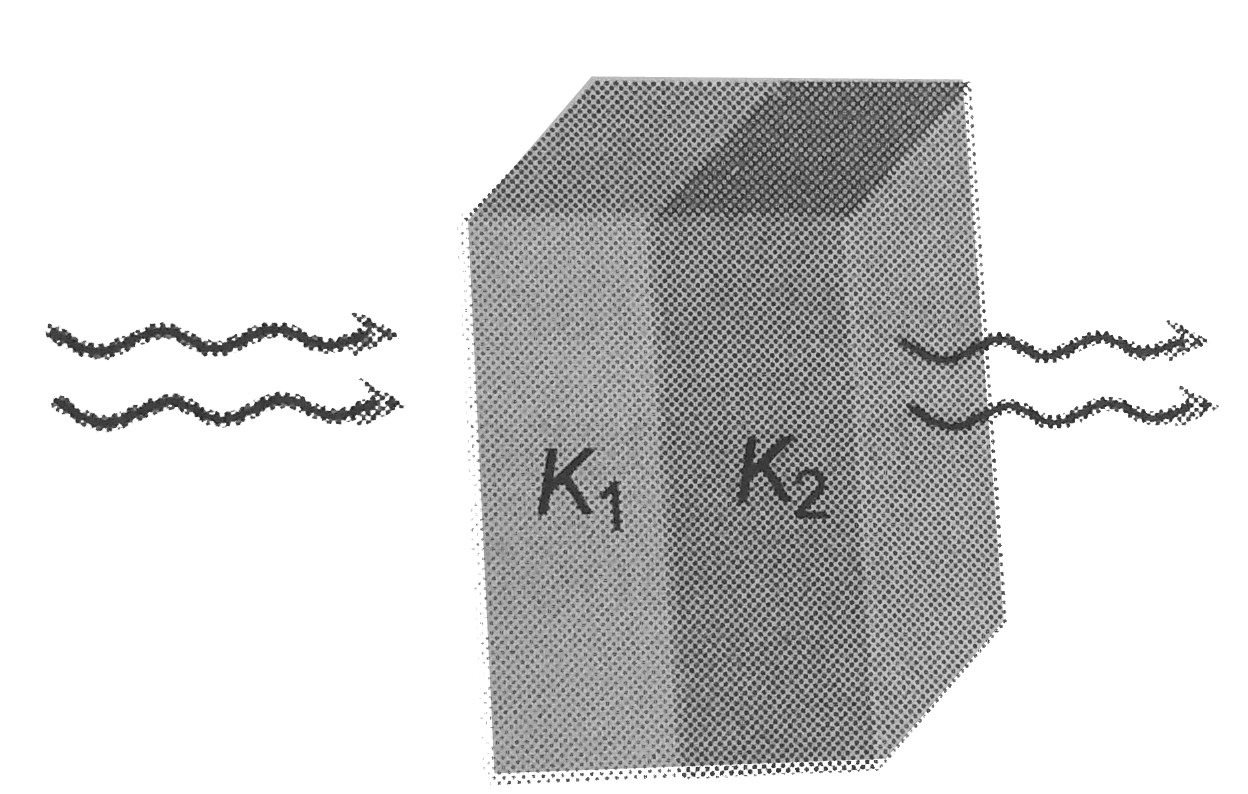
2K=1K1+1K2
if K1<K2
then K1<K<K2
Hence assertion and reason both are false.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - NEET Questions
47 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test
28 Videos
Similar Questions
Define coefficient of thermal conductivity. Two metal slabs of same area of cross-section, thickness d1 and d2 having thermal conductivities K1 and K2 respectively are kept in contact. Deduce expression for equivalent thermal conductivity.
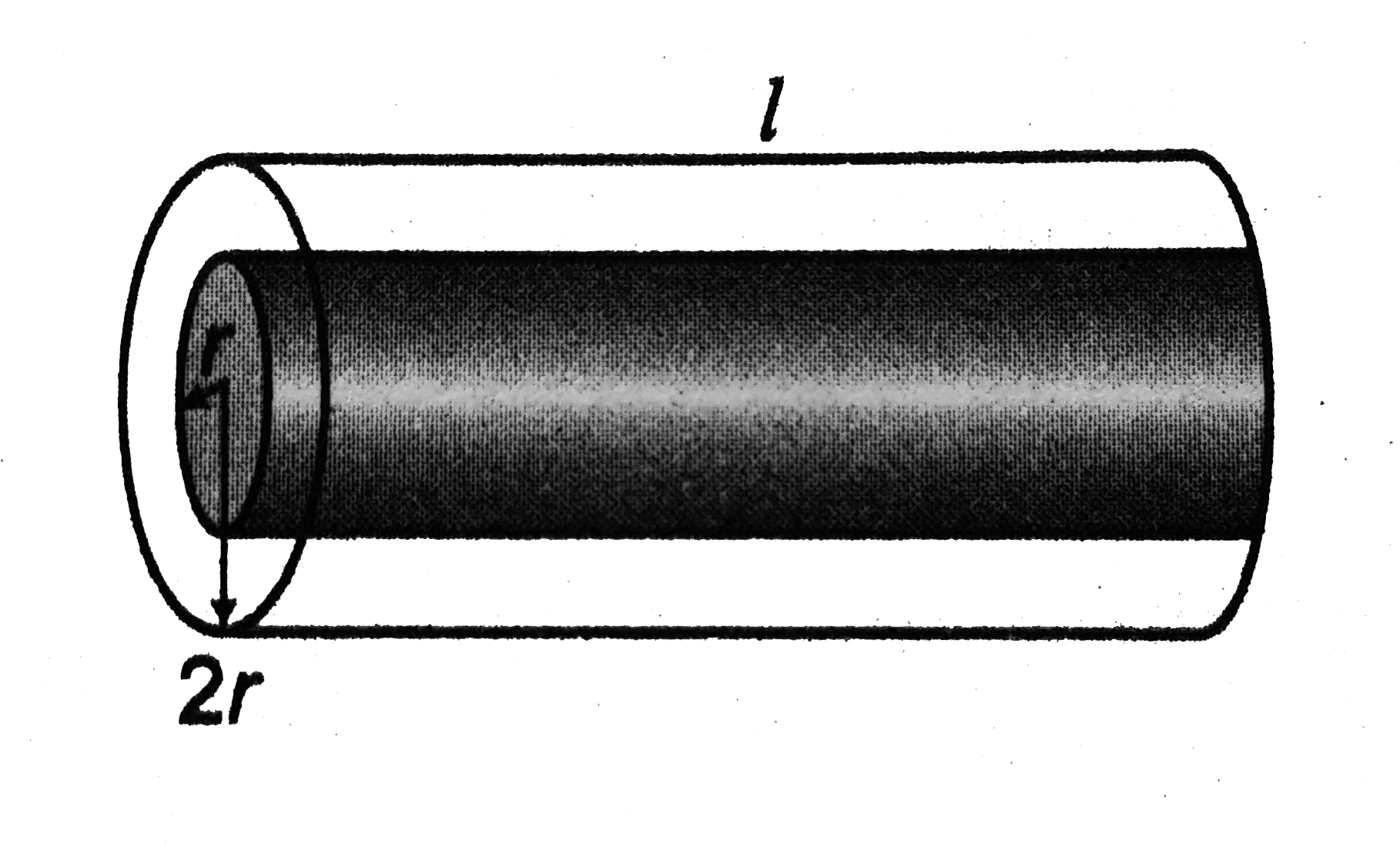
View SolutionThermal conductivity of inner core of radius r is K and of the outer one of radius 2r is 2K. Find equivalent value of thermal conductivity between its two ends.
View Solution
Knowledge Check
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2AStatement I is true, Statement II is true and Statement II is the correct explanation for statement I.BStatement I is true, statement II is true and statement II NOT the correct explanation for Statement ICStatement I is true, Statement II is false.DStatement I is false, statement II is true.Two rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
AK1K2K1+K2B(K1+K2)CK1+K22D√K1K2Two rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
AK1K2K1+K2B(K1+K2)CK1+K22D√K1K2
Two identical metal wires of thermal conductivities K1 and K2 respectively are connected in series. The effective thermal conductivity of the combination is :
View SolutionThe thermal resistances of two slabs are 3 and 2 units. When connected in series, the equivalent thermal resistance will be
View SolutionIf two metallic plates of equal thickness and thermal conductivities K1 and K2 are put together face to face and a common plate is constructed, then the equivalent thermal conductivity of this plate will be
View SolutionIf two metallic plates of equal thickness and equal length and thermal conductivities K1andK2 are put together face to face a common plate is constructed, then the equivalent thermal conductivity of this plate will be-
View SolutionTwo rods of the same length and diameter, having thermal conductivities K1 and K2, are joined in parallel. The equivalent thermal conductivity to the combinationk is
View Solution