A copper block of mass 2.5kg is heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount (approx.) of ice that can melt? (Specific heat copper =0.39J/g∘C heat of fusion of water =335J/g).
2kg
1.5kg
2.5kg
0.5kg
The correct Answer is:B
To solve the problem of how much ice can be melted by a copper block heated to 500°C, we can follow these steps:
Step 1: Calculate the heat lost by the copper block
The heat lost by the copper block when it cools down to 0°C can be calculated using the formula:
Q=m⋅c⋅ΔT
Where:
- Q = heat lost (in joules)
- m = mass of the copper block (in grams)
- c = specific heat capacity of copper (in J/g°C)
- ΔT = change in temperature (in °C)
Given:
- Mass of copper block, m=2.5kg=2500g
- Specific heat of copper, c=0.39J/g°C
- Initial temperature of copper, Ti=500°C
- Final temperature of copper, Tf=0°C
The change in temperature, ΔT=Ti−Tf=500−0=500°C.
Now substituting the values into the formula:
Q=2500g⋅0.39J/g°C⋅500°C
Calculating this gives:
Q=2500⋅0.39⋅500=487500J
Step 2: Calculate the mass of ice that can be melted
The heat required to melt ice can be calculated using the formula:
Q=m⋅L
Where:
- Q = heat absorbed by the ice (in joules)
- m = mass of ice melted (in grams)
- L = latent heat of fusion of ice (in J/g)
Given:
- Latent heat of fusion of ice, L=335J/g
Now we can rearrange the formula to find the mass of ice melted:
m=QL
Substituting the values we have:
m=487500J335J/g
Calculating this gives:
m≈1455.22g
Step 3: Convert grams to kilograms
To express the mass in kilograms:
m≈1.455kg
Conclusion
The maximum amount of ice that can melt is approximately 1.455 kg, which can be rounded to 1.5 kg.
The heat lost by the copper block when it cools down to 0°C can be calculated using the formula:
- Q = heat lost (in joules)
- m = mass of the copper block (in grams)
- c = specific heat capacity of copper (in J/g°C)
- ΔT = change in temperature (in °C)
- Mass of copper block, m=2.5kg=2500g
- Specific heat of copper, c=0.39J/g°C
- Initial temperature of copper, Ti=500°C
- Final temperature of copper, Tf=0°C
The heat required to melt ice can be calculated using the formula:
- Q = heat absorbed by the ice (in joules)
- m = mass of ice melted (in grams)
- L = latent heat of fusion of ice (in J/g)
- Latent heat of fusion of ice, L=335J/g
To express the mass in kilograms:
The maximum amount of ice that can melt is approximately 1.455 kg, which can be rounded to 1.5 kg.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Transmission Of Heat : Conduction
Explore 28 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Transmission Of Heat : Radiation
Explore 28 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBook:A2ZChapter:UNIT, DIMENSION AND ERROR ANALYSISExercise:Chapter Test
Explore 28 Videos
Similar Questions
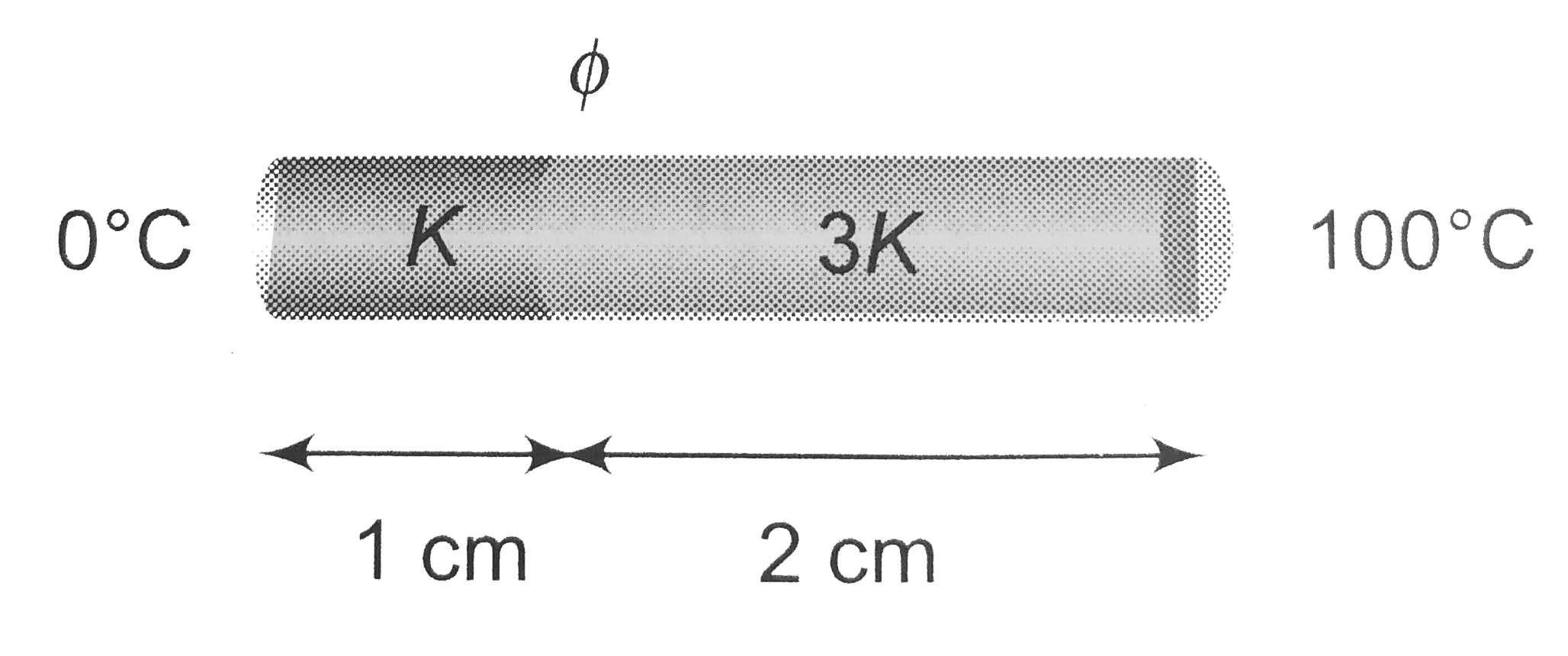
Two bars of thermal conductivities K and 3K and lengths 1cm and 2cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite bar is 0∘C and K2/l respectively (see figure), then the temperature ϕ of the interface is
View SolutionThe rectangular surface of area 8cm×4cm of a black body at temperature 127∘C emits energy E per section if length and breadth are reduced to half of the initial value and the temperature is raised to 327∘C, the ratio of emission of energy becomes
View SolutionIf mass-energy equivalence is taken into account, when water is cooled to from ice, the mass of water should
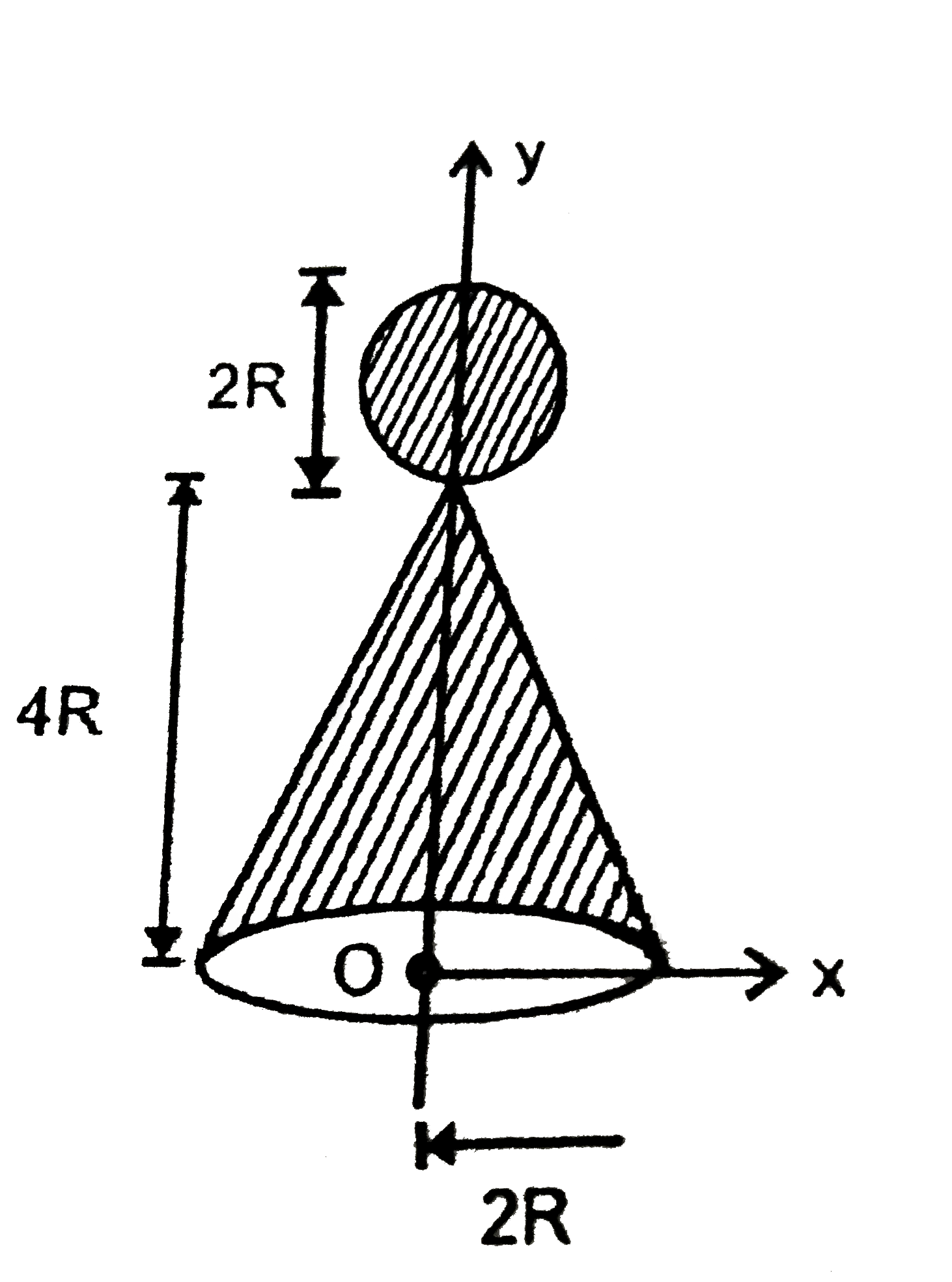
View SolutionA carpenter has constructed a toy as shown in figure. If the density of the material of the sphere is 12 tirnes that of cone, the y− coordinate of COM of toy point O
View SolutionThe dimensions of shear modulus are
View Solution2.5 kg द्रव्यमान के ताँबे के गुटके को किसी भट्ठी में 500∘ C तक तप्त करने के पश्चात् किसी बड़े हिम-ब्लॉक पर रख दिया जाता है | गलित हो सकने वाली हिम की अधिकतम मात्रा क्या है ? ताँबे की विशिष्ट ऊष्मा धारिता = 0.39Jg−1K−1 , बर्फ की संगलन ऊष्मा =335Jg−1 |
View SolutionA 2 kg copper block is heated to 500∘C and then it is placed on a large block of ice at 0∘C. If the specific heat capacity of copper is 400J/kg/∘C and latent heat of fusion of water is 3.5×105 J/kg. The amount of ice that can melt is :
View SolutionA copper block of mass 2.5 kg is heated in a furance to temperature of 500∘C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper =380Jkg−1K−1, latetn heat of fusion of ice =3.36×105Jkg−1).
View SolutionA copper block of mass2.5 kg ts heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper = 0.39Jg−1K−1, heat of fusion of water =335Jg−1).
View SolutionA copper block of mass2.5 kg ts heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper = 0.39Jg−1K−1, heat of fusion of water =335Jg−1).
View SolutionA copper block of mass2.5 kg ts heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper = 0.39Jg−1K−1, heat of fusion of water =335Jg−1).
View SolutionA copper block of mass2.5 kg ts heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper = 0.39Jg−1K−1, heat of fusion of water =335Jg−1).
View SolutionA copper block of mass 2.5kg is heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount (approx.) of ice that can melt? (Specific heat copper =0.39J/g∘C heat of fusion of water =335J/g).
View SolutionA copper block of mass 2.5 kg is heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount of ice that can melt ? (Specific heat of copper =0.39 Jg−1K−1, heat of fusion of water =335 Jg−1).
View Solution2.5kg ਪੁੰਜ ਦੇ ਤਾਂਬੇ ਦਾ ਗੁਟਕੇ ਨੂੰ ਕਿਸੇ ਭੱਠੀ ਵਿਚ 500∘C ਤਕ ਗਰਮ ਕਰਨ ਤੋਂ ਬਾਅਦ ਕਿਸੇ ਵੱਡੇ ਬਰਫ਼ ਦੇ ਬਲਾਨ ਤੇ ਰੱਖ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ। ਬਰਫ਼ ਦੇ ਪਿਘਲਣ ਵਾਲੀ ਅਧਿਕਤਮ ਮਾਤਰਾ ਕੀ ਹੈ? ਤਾਂਬੇ ਦੀ ਵਿਸ਼ਿਸ਼ਟ ਤਾਪ ਊਰਜਾ ਧਾਰਣ ਸਮਰੱਥਾ=0.39Jg−1K−1 , ਬਰਫ਼ ਦੀ ਸੰਗਲਣ ਊਰਜਾ= 335Jg−1 ਹੈ।
View Solution

