A body of mass 0.4kg starting at origin at t=0 with a speed of 10ms−1 in the positive x-axis direction is subjected to a constant F=8 N towards negative x-axis.
−6000m
−8000m
+4000m
+7000m
The correct Answer is:A
To solve the problem step by step, we will follow the laws of motion and apply the relevant equations.
Given Data:
- Mass of the body, m=0.4kg
- Initial velocity, u=10m/s (in the positive x-direction)
- Force acting on the body, F=−8N (towards the negative x-direction)
- Time, t=25s
Step 1: Calculate Acceleration
Using Newton's second law of motion, we can calculate the acceleration a using the formula:
F=m⋅a⟹a=Fm
Substituting the values:
a=−8N0.4kg=−20m/s2
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity.
Step 2: Calculate Displacement
We will use the equation of motion to calculate the displacement s:
s=ut+12at2
Substituting the values:
s=(10m/s)(25s)+12(−20m/s2)(25s)2
Calculating each term:
1. ut=10×25=250m
2. 12at2=12×(−20)×(252)=−10×625=−6250m
Now substituting back into the displacement equation:
s=250−6250=−6000m
Conclusion
The displacement of the body after 25 seconds is −6000m, indicating that the body has moved 6000 meters in the negative x-direction.
Final Answer
The displacement is −6000m.
---
- Mass of the body, m=0.4kg
- Initial velocity, u=10m/s (in the positive x-direction)
- Force acting on the body, F=−8N (towards the negative x-direction)
- Time, t=25s
Using Newton's second law of motion, we can calculate the acceleration a using the formula:
F=m⋅a⟹a=Fm
Substituting the values:
a=−8N0.4kg=−20m/s2
The negative sign indicates that the acceleration is in the opposite direction to the initial velocity.
We will use the equation of motion to calculate the displacement s:
s=ut+12at2
Substituting the values:
s=(10m/s)(25s)+12(−20m/s2)(25s)2
Calculating each term:
1. ut=10×25=250m
2. 12at2=12×(−20)×(252)=−10×625=−6250m
s=250−6250=−6000m
The displacement of the body after 25 seconds is −6000m, indicating that the body has moved 6000 meters in the negative x-direction.
The displacement is −6000m.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Linear Momentum And Impulse
Explore 20 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Equilibrium Of A Particle
Explore 19 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
A body of mass 0 .40 kg moving intially with a constant speed of 10m/s to the north is subjected to a constant force of 8.0 N directed towards the south for 30 s Take the instant the force is applied to be t = 0 , and the position of the particle at that time to be x = 0 , predict its position at t=−5s,25s,100s ?
View SolutionA ball of mass 0.2 kg travelling in a straight line with a speed of m/s along negative x- axis id deflected by a bat 15m/s along negative x - axis is deflected by a bat at an angle of 30∘ If the speed of the ball after deflection is 10m/s, find the impulse on the ball.
View Solution
Knowledge Check
A body of mass m=3.513kg is moving along the x-axis with a speed of 5.00ms−1. The magnetude of its momentum is recorded as
A(a) 17.6kgms−1B(b) 17.565kgms−1C(c) 17.56kgms−1D(d) 17.57kgms−1A block of mass 20 kg is moving in x-direction with a constant speed of 10ms−1. It is subjected to a retarding force F=(−0.1x)N during its travel from x=20m to x=30m. Its final kinetic energy will be
A975 JB450 JC275 JD250 JThe inclination of the line x−y+3=0 with the positive direction of x-axis is
A45∘B135∘C−45∘D−135∘
A body of mass 0.4 kg is whirled in a horizontal circle of radius 2 m with a constant speed of 10ms−1. Calculate its frequency of revolution.
View SolutionA particle of mass m is at rest at the origin at time t=0. It is subjected to a force F(t)=F0e−bt in the X - direction. Its speed V(t) is depicted by which of the following curves.
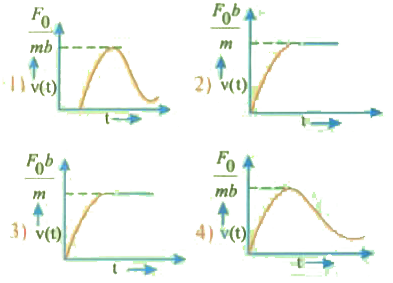
View SolutionA block of mass 20 kg is moving in x-direction with a constant speed of 10 ms−1. It is subjected to a retarding force F=(−0.1x)N during its travel from x=20 m to x=30 m. Its final kinetic energy will be
View SolutionA particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionA block of mass 10 kg is moving in x-direction with a constant speed of 10ms−1. It is subjected to a retarding force F=−0.1xJm−1 during its travel from x = 20 m to x = 30 m. Its final kinetic energy will be
View Solution

