A paricle starting from the origin (0,0) moves in a straight line in (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

A

30∘

B

45∘

C

60∘

D

0∘

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:c

Slope of the path of the particle gives the measure of angle required.
Draw the situation as shown. OA represents the path of the particle starting from origin O(0,0). Draw a perpendicular from point A to x-axis. Let path of the particle makes an angle θ with the x-axis, then
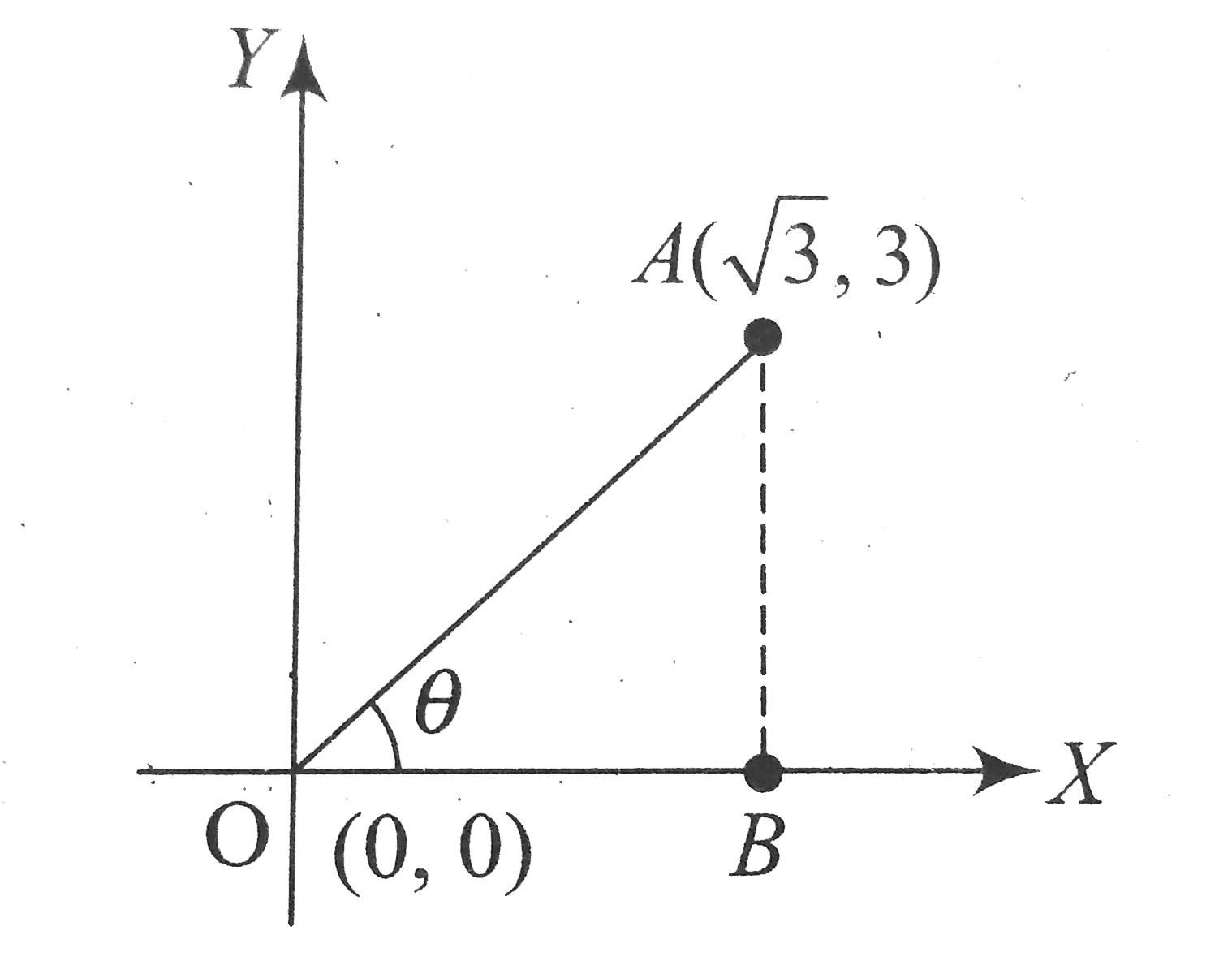
ocr_image
tanθ=slope of line OA=ABOB=3√3=√3
or θ=60∘

Updated on:21/07/2023
|
Class 11PHYSICSPROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A particle starting from the origin (0,0) moves in a straight line in the (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

    A30∘
    B45∘
    C60∘
    D0∘

  • A particle starting from the origin (0,0) moves in a straight line in the (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

    A30∘
    B45∘
    C60∘
    D0∘

  • A paricle starting from the origin (0,0) moves in a straight line in (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

    A45∘
    B60∘
    C0∘
    D30∘