Two point particles with masses m1andm2 are thrown at angles θ1andθ2 with horizontal with speeds v1andv2 respectively. R, H and T are range, height and total time of flight respectively. Let v1sinθ1=v2sinθ2. Then for both particles
T,H and R are different
H and R will be same but T will be different
T and R are same but H will be different
T and H are same but R is different.
The correct Answer is:D
Relations for,
T=2usinθg,R=u2sin2θgandH=u2sin2θ2g
Here, u1sinθ1=u2sinθ2
T and H are same but will not be same.
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Assertion Reasoning
11 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NEET Questions
16 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Kinematics Of Circular Motion
26 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
Two objects with masses m1andm2 are moving along the x-axis in the positive direction with speeds v1,andv2 , respectively, where v1 is less than v2 . The speed of the centre of mass of this system of two bodies is
Agreater than v2BEqual to v1Cequal to the average of v1andv2Dgreater than v1 and less than v2Two particles are projected simultaneously in the same vertical plane from the same point, with different speeds u1 and u2, making angles θ1 and θ2 respectively with the horizontal, such that u1cosθ1=u2cosθ2. The path followed by one, as seen by the other (as long as both are in flight), is
AA parabolaBA vertical straight lineCA horizontal straight lineDnone of aboveTwo projectivles are thrown simultaneously in the same plane from the same point. Iff their velocities are v1andv2 at angles θ1andθ2 respectively from the horizontal, then answer the following questions.
Q. If v1sinθ1=v2sinθ2, then choose the incorrect statementAThe time of flight of both the particles will be sameBThe maximum height attained by the particles will be sameCThe trajectory of one with respect to another will be a horizontal straight lineDNone of these
Two particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
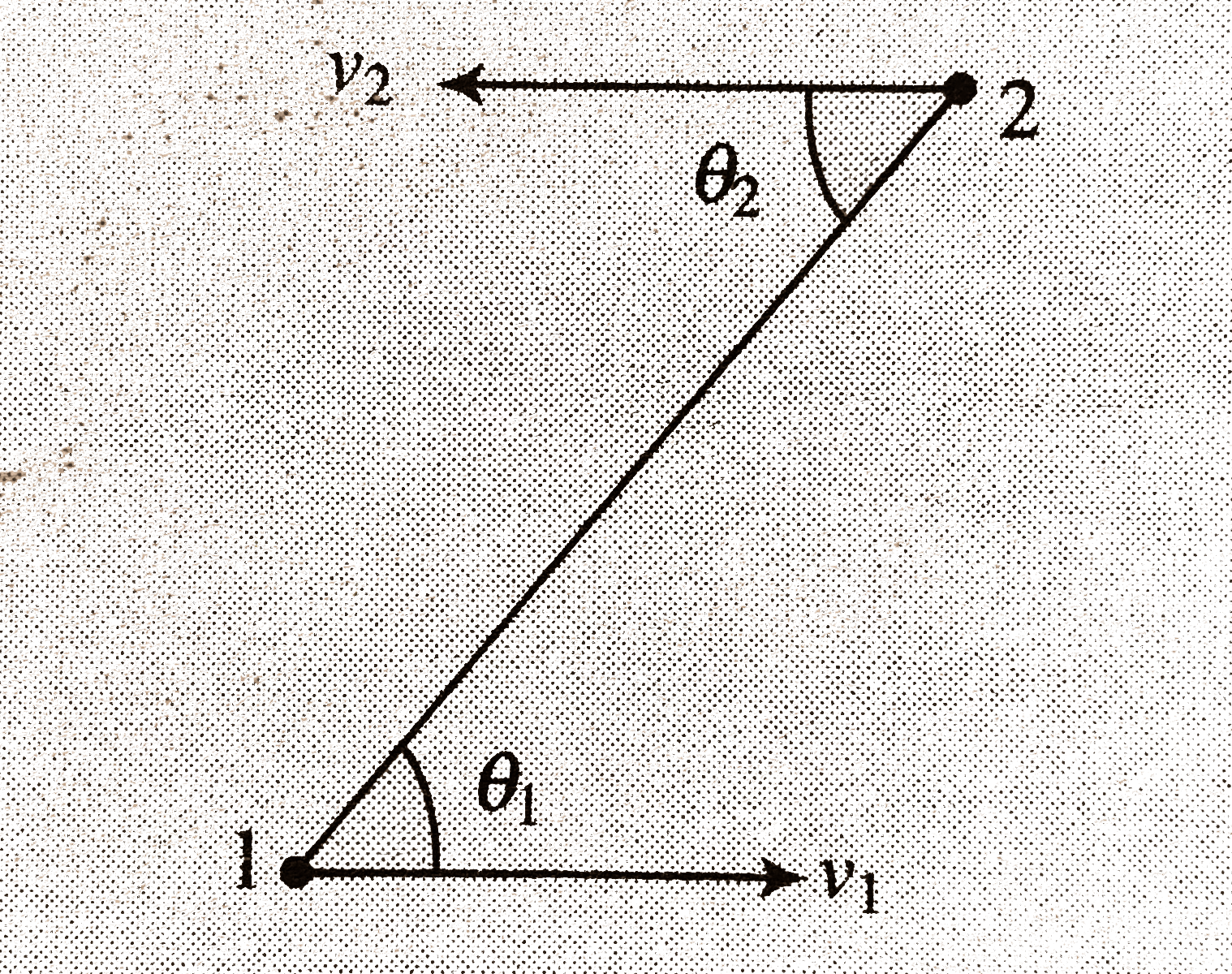 .
.
View SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
If v1cosθ1=v2cosθ2, then choose the incrorrect statement
View SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at anglesθ1 and θ2 respectively from the horizontal, then answer the following questions.
If v1cosθ1=v2cosθ2, then choose the incorrect statement
View SolutionTwo projectivles are thrown simultaneously in the same plane from the same point. Iff their velocities are v1andv2 at angles θ1andθ2 respectively from the horizontal, then answer the following questions.
Q. If v1=v2andθ1>θ2, then choose the incorrect statement
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 and θ2 to the horizontal. If their respective times of flights are T1 and T2 and horizontal ranges are same then
a) θ1+θ2=90∘ ,
b)T1=T2tanθ1
c.T1=T2tanθ2 ,
d) T1sinθ2=T2sinθ1
View Solution

