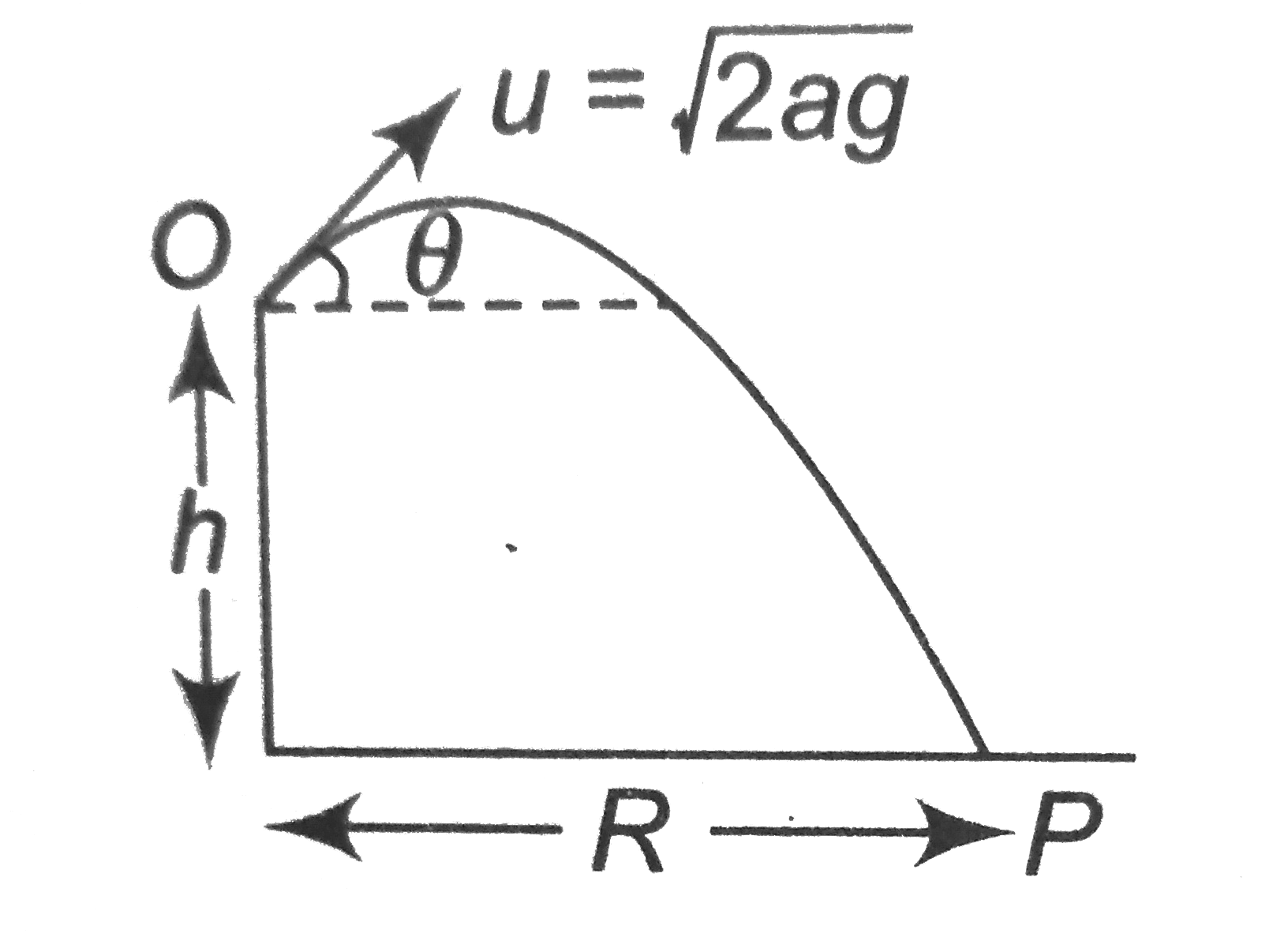
A particle is projected under gravity with velocity √2ag from a point at a height h above the level plane at an angle θ to it. The maximum range R on the grond is :
√(a2+1)/h
√(a2h)
√(ah)
2√a(a+h)
The correct Answer is:d
Coordinate of point P are (R,-h)
Hence −h=Rtanθ−gR22(2ga)(1+tan2θ)
or R2tan2θ−4aRtanθ+(R2−4ah)=0
For θ to be real.
(4aR2)≥4R2(R2−4ah)
or 4a2≥(R2−4ah)
or R2≤4a(a+h)
Rmax=2√a(a+h)
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Projection From Inclined Plane
Explore 20 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Relative Velocity In Two Dimensions
Explore 23 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Motion With Constant Acceleration
Explore 15 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
A particle is projected vertically upwards from O with a velocity and a second particle is projected at the same instant from P (at a height h above O) with velocity v at an angle of projection θ with the horizontal. Find the time when the distance between them is minimum. Take v=5m/s and h=20m
View SolutionA particle in projected with velocity √3gL at point A (lowest point of the circle) in the vertical plane. Find the maximum height about horizontal level of point A if the string slacks at the point B as shown in figure.

View Solution
Knowledge Check
A particle is projected vertically upwards from the ground with a speed V and a speed v and a second particle is projected at the same instant from a height h directly above the first particle with the same speed v at an angle of projection θ with the horizontal in upwards direction. The time when the distance between them is minimum is
Ah2υsinθBh2υcosθCh/υDh2υA particle is to be projected horizontally with velocity v from a point P, which is 60m above the foot of a plane inclined at angle 45∘ with horizontal as shown in figure. The particle hits the plane perpendicularly at A. After rebound from inlined plane it again hits at B. If coefficient of restitution between particles and plane is 1√2 then,
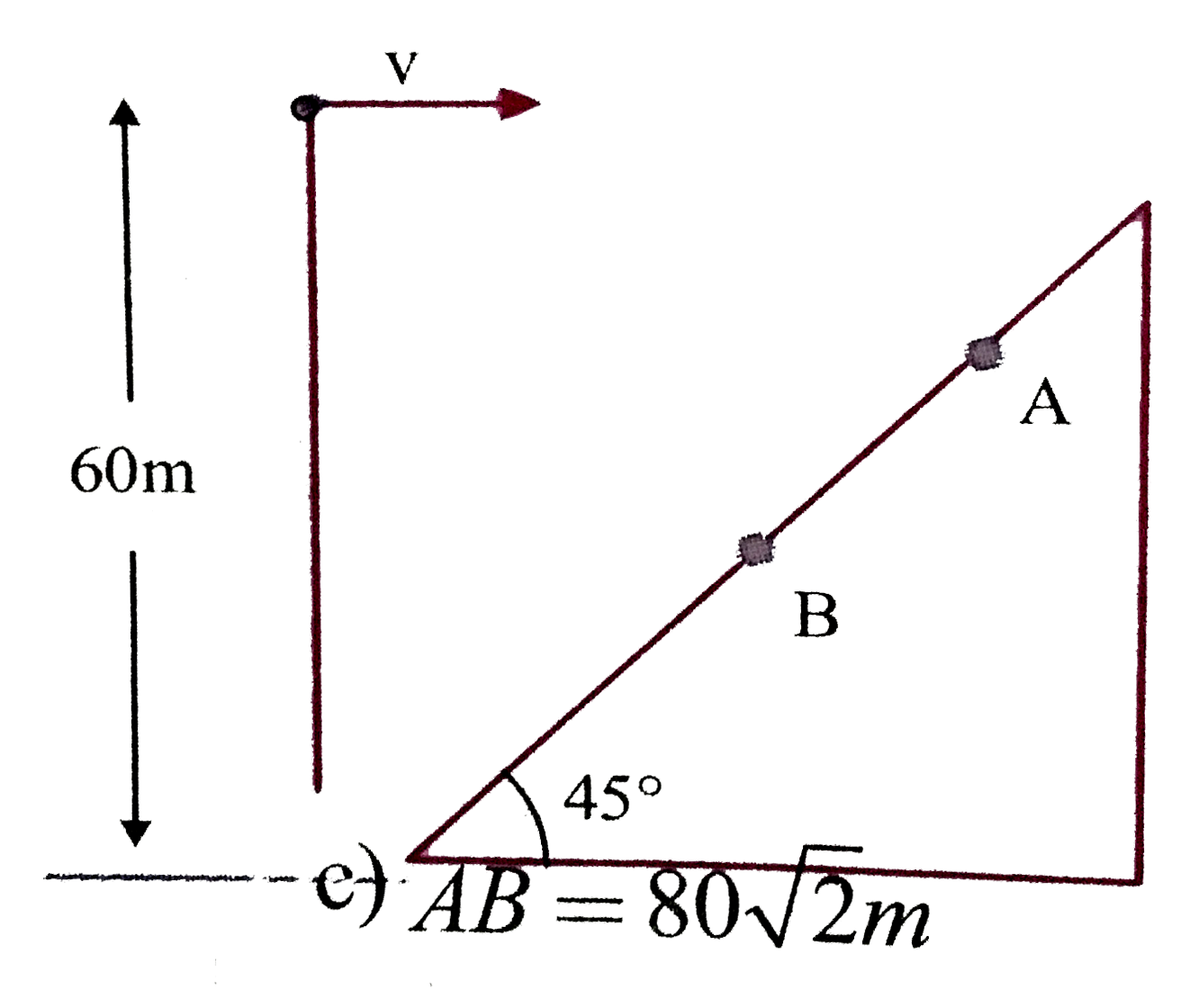 Av=20m/sBv=10m/sCAB=80√2mDAB=80m
Av=20m/sBv=10m/sCAB=80√2mDAB=80mA particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
AR2BRC2RD5R4
A particle is projected with a velocity u from a point at ground level. Show that it cannot clear a wall of height h at a distance x from the point of projection if u2<g(h+√h2+x2).
View SolutionA particle is projected with velocity 2√ag so that it just clears two walls, of equal height a, at a distance 2a from each other . Show that the velocity of projection is 60∘ and that the latus rectum of the path is 2a.
View SolutionA particle is projected from the top of a tower of height H. Initial velocity of projection is u at an angle θ above the horizontal . Particle hits the ground at a distance R from the bottom of tower. What should be the angle of projection θ so that R is maximum ? What is the maximum value of R?
View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA particle is projected with a velocity v such that its range on the horizontal plane is twice the greatest height attained by it. The range of the projectile is (where g is acceleration due to gravity)
View Solution

