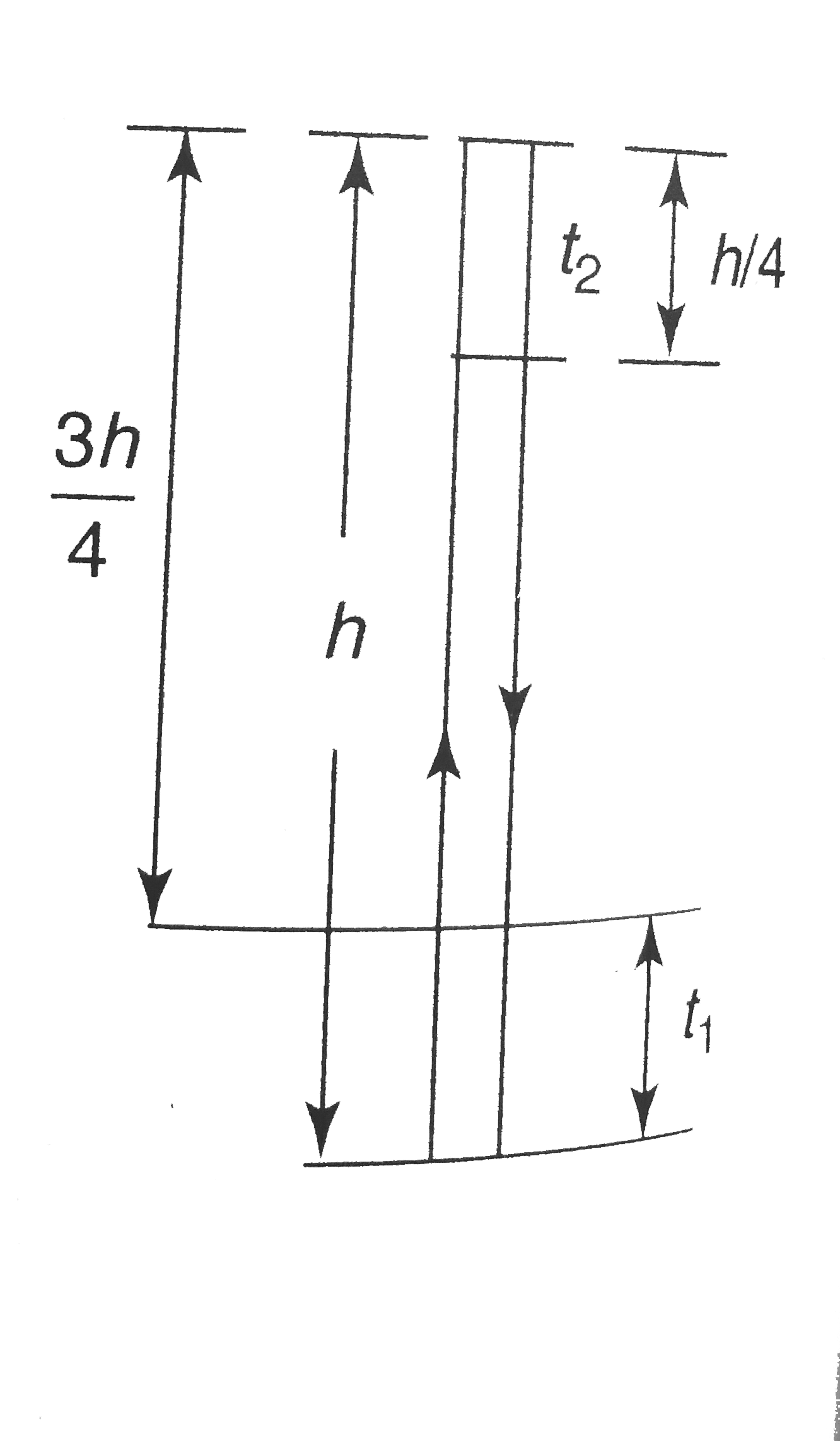
A body projected vertically upwards with a given velocity. The ratio of the times taken to cover the first one fourth and the last one fourth of the ascent to the highest point is.
A
1:(2−√3)
B
2:(2−√3)
C
(2−√3):1
D
(2−√3):2
Video Solution
Text Solution
The correct Answer is:C
t2=√2(h/4)g
t2=√h2g
t1=√2hg−√2(3h)g
=√h2g[2−√3]
t1:t2=(2−√3):1.
|
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Relative Motion In One Dimension
Explore 20 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Understanding Motion Through Graphs
Explore 40 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Motion With Constant Acceleration
Explore 30 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Chapter Test
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
A body is projected vertically upwards with some velocity u. It is at the same point at t=6s as was at t=4s. Find the value of u.
A30m/sB40m/sC20m/sD50m/sA body projected vertically upwards with a velocity u returns to the starting point in 4 seconds. If g=10m/sec, the value of u is
A5m/secB10m/secC15m/secD20m/secA body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A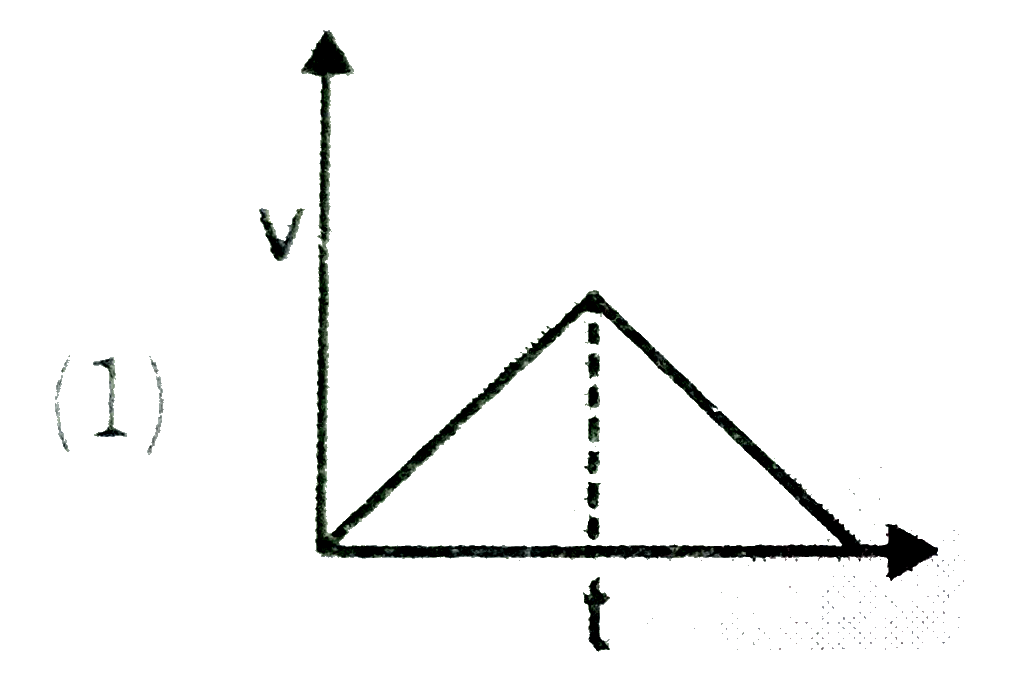 B
B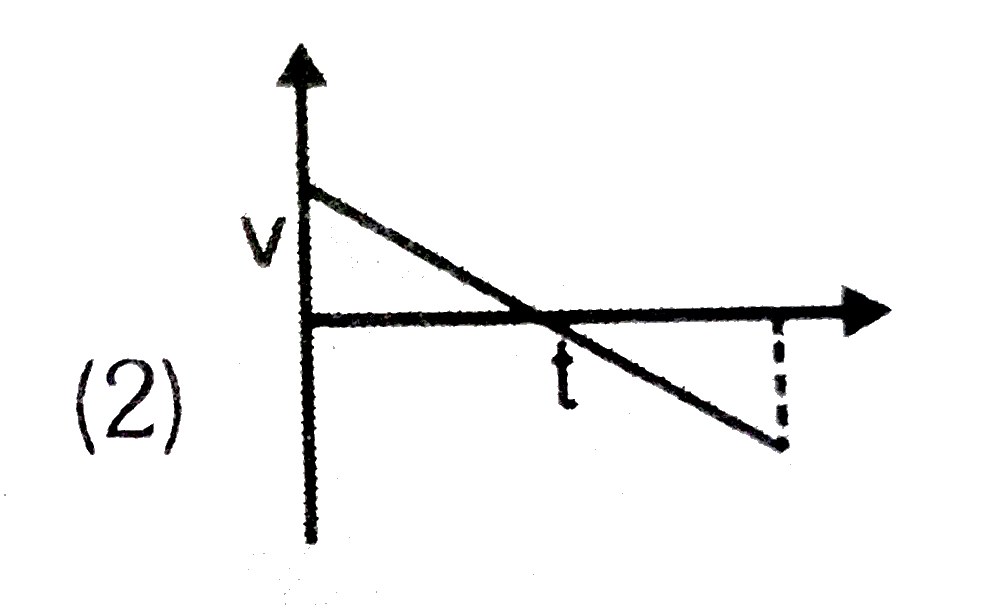 C
C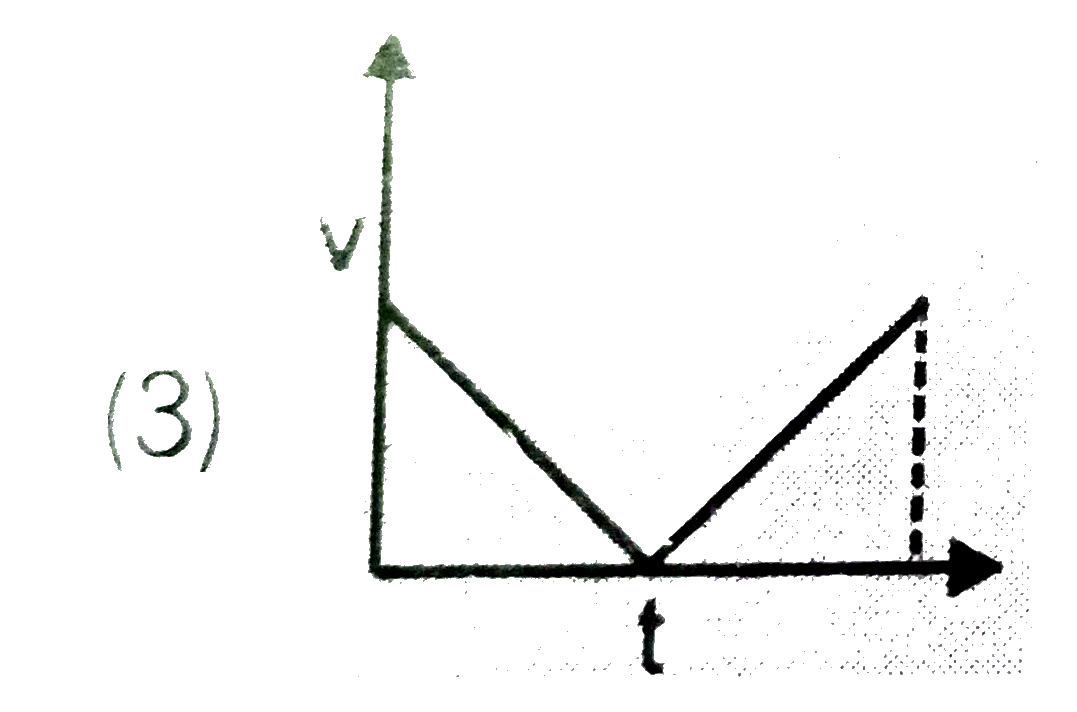 D
D
A ball is projected vertically upward with a velocity 112m/s The time taken by it to return to the point of projection is (g=10m/s2) :
View SolutionA ball is projected vertically upward with a velocity 112m/s The time taken by it to return to the point of projection is (g=10m/s2) :
View SolutionA ball is thrown vertically upward. What is the magnitude of velocity at the highest point ?
View SolutionA player throws a ball vertically upwards with velocity u. At highest point,
View SolutionA particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
View Solution

