Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres ? Use the reuslt obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions. Solution in Telugu
The charge flows from the sphere at higher potential to the other at lower potential till their potentials become equal. After sharing the charges on two spheres would be.
Q1Q2=C1VC2V Where C1.C2 are the capacities of two spheres.
But C1C2=ab∴Q1Q2=ab
Ratio of surface density of charge on the two spheres
σ1σ2=Q14πa2×4πb2Q2=Q1Q2.b2a2=(ab)(b2a2)=ba
Hence ratio of electric fields at the surface of two spheres
E1)E2=σ1σ2=ba
A sharp and potential end can be treated as a sphere of very small radius and a flat portion behaves as a sphere of much larger radius. Therefore, charge density on sharp and pointed ends of conductor is much higher than on its flatter portions.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Textual Examples
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Important Questions
Explore 3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Textual Exercises
Explore 11 Videos
- ELECTROMAGNETIC WAVEBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:ELECTROMAGNETIC WAVEExercise:ADDITIONAL EXERCISES
Explore 19 Videos
- MAGNETISM AND MATTERBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:MAGNETISM AND MATTERExercise:Additional Exercises
Explore 19 Videos
Similar Questions
Figure (a) and (b) shows the field lines of a positive and negative point charge respectively.
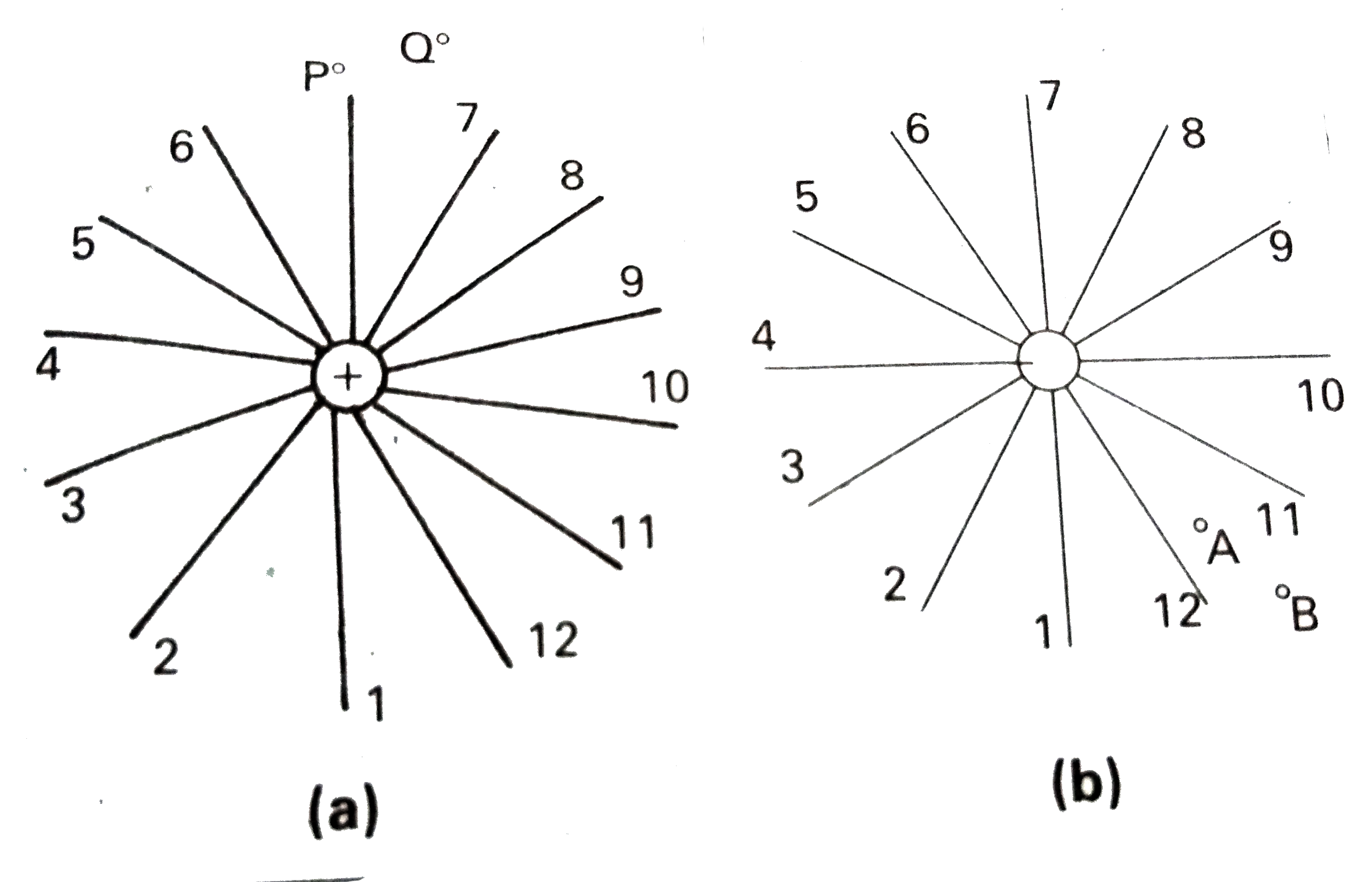
Give the signs of the potential difference Vp−VQ,VB−VA.
View SolutionThree capacitors of capacitances 1muF,2muF and 3muFare connected in parallel
(a) What is the ratio of charges ?
(b) What is the ratio of potential differences ?
View SolutionTwo charges 5×10−8Cand−3×10−8C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
View SolutionSuppose that the electric field part of an electromagnetic wave in vacuum is E={(3.1 N/C) cos [(1.8 rad/m)y+{5.4×106 rad/s} t]} i.
What is the direction of propagation ?
View SolutionWhy does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled?
View SolutionTwo charged conducting spheres of radill a and b are connected to eachother by a wire. What is the ratio of electric fields at the surface of two spheres ? Use the result obtained to explain why charge density on the sharp and pointed ends of a conducter is higher than on its fatter portions ?
View Solutiona और b त्रिज्याओं वाले दो आवेशित चालक गोले एक तार द्वारा एक-दूसरे से जोड़े गए हैं। दोनों गोलों के पृष्ठों पर विद्युत क्षेत्रों में क्या अनुपात है? प्राप्त परिणाम को, यह समझाने में प्रयुक्त कीजिए कि किसी एक चालक के तीक्ष्ण और नुकीले सिरों पर आवेश घनत्व, चपटे भागों कि अपेक्षा अधिक क्यों होता है ।
View Solutiona और b त्रिज्याओं वाले दो आवेशित चालक गोले एक तार द्वारा एक-दूसरे से जोड़े गए हैं। दोनों गोलों के पृष्ठों पर विद्युत क्षेत्रों में क्या अनुपात है? प्राप्त परिणाम को, यह समझाने में प्रयुक्त कीजिए कि किसी एक चालक के तीक्ष्ण और नुकीले सिरों पर आवेश घनत्व, चपटे भागों की अपेक्षा अधिक क्यों होता है?
View SolutionTwo charge conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric field at the surfaces of the two spheres ?
View SolutionTwo charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
View SolutionTwo charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
View SolutionTwo charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
View SolutionTwo charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
View SolutionTwo charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surface of two spheres ? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its fatter portions ?
View SolutionTwo charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres ? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
View Solution

