Question

Find the number of 4- digit numbers that can be formed using the digits 1,2,3,4,5,6 that are divisible by (i) 2 (ii) 3 when repetition is allowed.

Explanation

(i) Numbers divisible by 2 Take 4 blank places, First the units place

Can be filled by an even digit in 3 ways (2 or 4 or 6). The remaining three places can be filled with the 6 digits in 6 ways each. Thus they cna be filled in `6xx6xx6=6^(3)` ways. Therefore, the number of 4 digited numbers divisible by is `3xx6^(3)=3xx216=648`
(ii) Number divisible by 3 First we fill up the first 3 places with the given 6 digits in `6^(3)` ways.

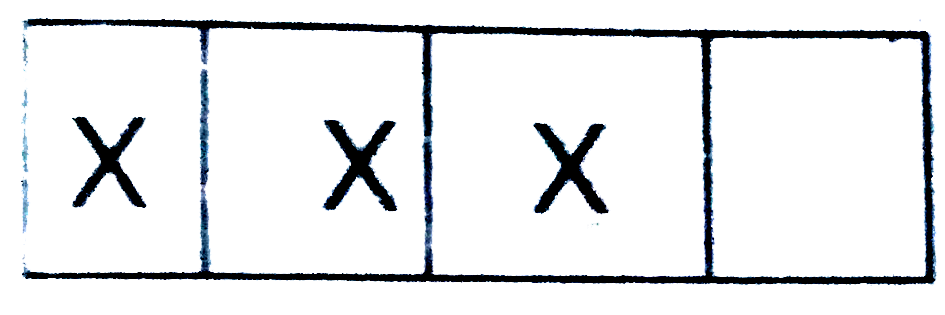
After filling up the first 3 places, if we fill the units place with the given 6 digits, we get 6 consecutive positive integers. Out of these six consecutive integers exactly 2 will be divisible by '3'. Hence the units place can be filled in '2' ways. Therefore, the number of 4 digited numbers divisible by 3.
`=6^(3)xx2=216xx2=432.`