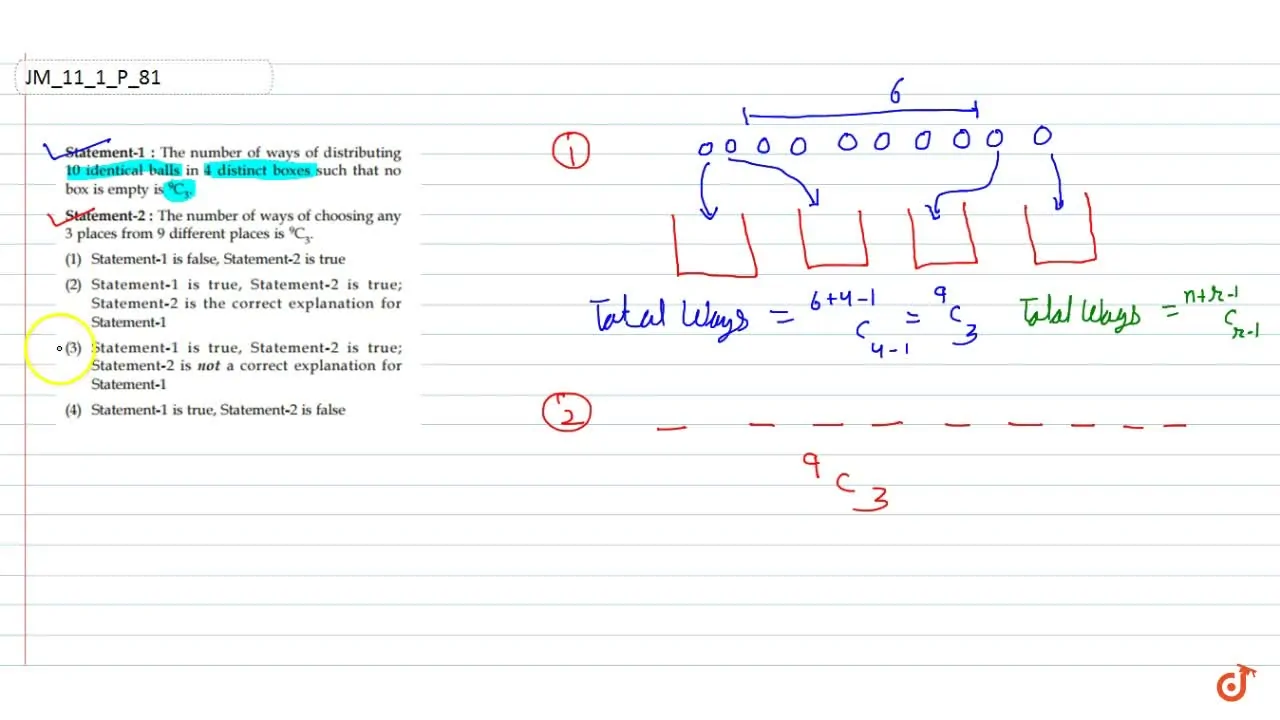
Statement-1 : The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is . Statement-2 : The number of ways of choosing any 3 places from 9 different places is . Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1. Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1. Statement-1 is true, Statement-2 is false. Statement-1 is false, Statement-2 is true.
1) total ways =
2)
option 3 is correct
Related Playlists
Similar Questions
Statement-1: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3.
Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3.View SolutionStatement-1: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3.
Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3.View SolutionLet A be a 2×2 matrix Statement 1 : adj(adjA)=A Statement 2 : |adjA|=|A| (1) Statement1 is true, Statement2 is true, Statement2 is a correct explanation for statement1 (2) Statement1 is true, Statement2 is true; Statement2 is not a correct explanation for statement1. (3) Statement1 is true, statement2 is false. (4) Statement1 is false, Statement2 is true
View SolutionStatement-1: ∫sin−1xdx+∫sin−1√1−x2dx=π2x+cStatement-2: sin−1x+cos−1x=π2 (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionStatement-1: The function F(x)=∫sin2xdx satisfies F(x+π)=F(x),∀ξnR ,Statement-2: sin2(x+π)=sin2x (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionStatement -1 (12)7<(13)4
⇒7log(12)<4log(13)⇒7<4
Statement-2 If ax<ay, where a<0,x,y>0, then x>y.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true.View SolutionIf A is 2 x 2 invertible matrix such that A=adjA−A−1 Statement-I 2A2+I=O(null matrix) Statement-II: 2|A|=1 (i) Statement-I is true, Statement-II is true; Statement-II is a correct explanation for Statement-I (2) Statement-I is true, Statement-II is true; Statement-II is not a correct explanation for Statement-I. 3) Statement-I is true, Statement-II is false. (4) Statement-I is false, Statement-II is true.
View SolutionLet f(x)={xnsin(1x),x≠0;0,x=0; and n>0 Statement-1: f(x) is continuous at x=0 and ∀n>0. and Statement-2: f(x) is differentiable at x=0 ∀n>0 (1) Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1. (2) Statement-1 is True, Statement-2 is True Statement-2 is NOT a correct explanation for Statement-1. (3) Statement-1 is True, Statement-2 is False (4) Statement-1 is False, Statement-2 is True.
View SolutionStatement-1: ∫(sinx)x(xcotx+logsinx)dx=x(sinx)xStatement-2: ddx(f(x))g(x)=(f(x))g(x)ddx[g(x)logf(x)] (A) Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. (B) Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1. (C) Statement-1 is True, Statement-2 is False. (D) Statement-1 is False, Statement-2 is True.
View SolutionLet A and B be two symmetric matrices of order 3. Statement-1 : A(BA) and (AB)A are symmetric matrices. Statement-2 : AB is symmetric matrix if matrix multiplication of A with B is commutative. Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1. Statement-1 is true, Statement-2 is true; Statement-2 is true; Statement-2 is not a correct explanation for Statement-1. Statement-1 is true, Statement-2 is false. Statement-1 is false, Statement-2 is true.
View Solution