A block of mass m at the end of a string is whirled round in a vertical circle of radius R. The critical speed of the block at the top of its swing below which the string would slacken before the block reaches the top is
Rg
(Rg)2
Rg
√Rg
At highest point mv2R=mg⇒v=√gR
Similar Questions
A stone of of mass 0 .25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40rev/min in a horizontal plane What is the tension in the string ? What is the maximum speed with which the stone can be whirled around If the string can withstand a maximum tension of 200 N ?
View SolutionA small body of mass m is tried to a string and revolved in a vertical circle of radius r. If the tension in the string at the highest point is mg, what is its speed there?
View Solution
Knowledge Check
A block of mass m at the end of a string is whirled round in a vertical circle of radius R. The critical speed of the block at top of its swing below which the string would slacken before the block reaches the bottom is?
A√5RgB√3RgC√2RgD√RgA stone at the end of 1m long string is whirled in a vertical circle at a constant speed of 4ms−1. The tension in the string is 6N when the stone is
A(a) 10ms−1B(b) 5√3ms−1C(c) 10√3ms−1D(d) 20ms−1A body of mass 2 kg attached to a cord and whirled in a verticle circle of radius 2 m. The minimum speed at the bottom of the circle so that the cord will not slacken when the body rounds the top of the circle will be (g=10m/s2)
A10m/sB6.3m/sC7m/sD5m/s
A body is mass m is rotating in a vertical circle of radius 'r' with critical speed. The difference in its K.E at the top and at the bottom is
View SolutionAn object of mass 10kg is attached to roof by string whirled round a horizontal circle of radius 4 and and and 30∘ to the vertical. The tension in the string (approximately) is
View SolutionA stone of mass of 1 kg is tied to the end of a string 1 m long. It is whirled in a vertical circle. The velocity of the stone at the bottom of the circle is just sufficient to take it to the top of circle without slackening of the string. What is the tension in the string at the top of the circle? (Take, g =10 ms−2)
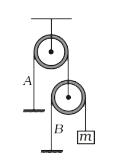
View SolutionThe block of mass m is at rest. Find the tension in the string A .
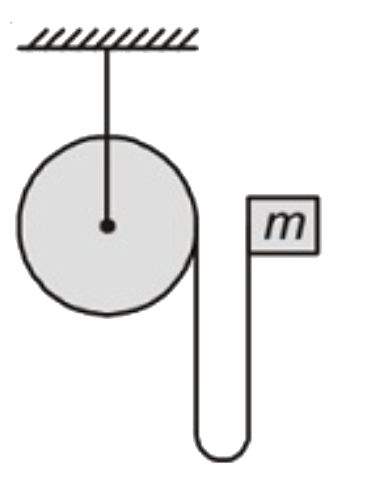
View SolutionA block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is 1. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
View Solution
