
Four identical metal butterflies are hanging from a light string of length 5l at equally placed points as shown. The ends of the string are attached to horizontal fixed support. The middle section of the string is horizontal . The relation between the angle θ1 and θ2 is given by
sinθ1=2sinθ2
2cosθ1=sinθ2
tanθ1=2tanθ2
θ2<θ1 and no other conclusion can be derived.
The correct Answer is:C

T1sinθ1=2mg
T2sinθ2=mg
T1cosθ1=T2cosθ2
2mgcotθ1=mgcotθ2
⇒tanθ1=2tanθ2
Similar Questions
A heavy particle hanging from a string of length l is projected horizontally with speed √gl. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View SolutionA block of mass M si suspended by two strings angles θ1 and θ2 with the horizontal. Find the tensions in the strings.

View Solution
Knowledge Check
A partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
Ak can never be geaater than 1Bk can never be less than 1Ck can never be equal than 1Dk can never be geaater than 3A particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
A√glB√2glC√3glD√5glIn the figure a mass m is hung by a light spring and a light string as shown .Both the spring and the string make an angle θ with the horizontal at equilbrium .If the string is suddenly cut then the instantaneous acceleration of the mass m is :
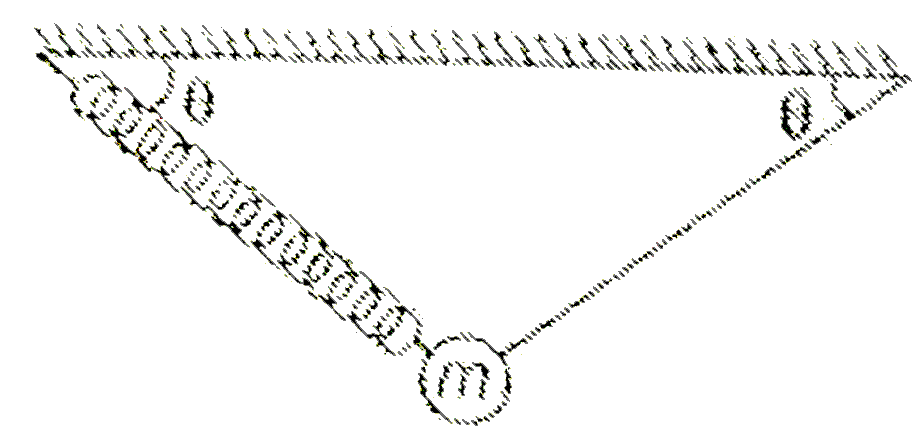 A2gsinθBgsinθCg2sinθDgcosθ
A2gsinθBgsinθCg2sinθDgcosθ
If a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View SolutionA disc of mass m lies flat on a smooth horizontal table. A light string runs halfway around it as shown in figure. One end of the string is attached to a particle of mass m and the other end is being pulled with a force F. There is no friction between the disc and the string. Find acceleration of the end of the string to which force is being applied.
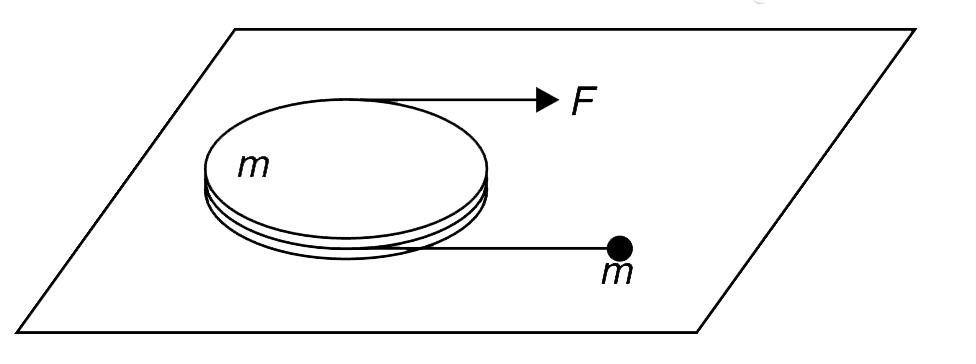
View SolutionA particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View SolutionA stone hanging from a massless string of length 15m is projected horizontally with speed √147ms−1 Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
View SolutionA stone hanging from a massless string of length 15m is projected horizontally with speed √147ms−1 Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
View Solution

