A spherical iron ball 10 cm in radius is coated with a layer of ice of unirform thichness that melts at a rate of 50cm3/min. when the thickness of ice is 5 cm, then the rate at which the thickness of ice decreases, is
154π cm/min
56π cm/min
136π cm/min
118π cm/min
The correct Answer is:D
To solve the problem, we need to find the rate at which the thickness of the ice decreases when the thickness is 5 cm. We will follow these steps:
Step 1: Define Variables
Let:
- r=10 cm (radius of the iron ball)
- x = thickness of the ice
- Total radius of the sphere with ice = R=r+x=10+x
Step 2: Volume of the Ice
The volume of the ice can be expressed as the volume of the larger sphere (iron ball + ice) minus the volume of the iron ball:
V=43π(R3)−43π(r3)
Substituting R=10+x and r=10:
V=43π((10+x)3−103)
Step 3: Differentiate Volume with Respect to Time
To find the rate at which the thickness of the ice decreases, we differentiate the volume V with respect to time t:
dVdt=ddt(43π((10+x)3−103))
Using the chain rule:
dVdt=43π⋅3(10+x)2⋅dxdt
This simplifies to:
dVdt=4π(10+x)2⋅dxdt
Step 4: Substitute Known Values
We know that the ice melts at a rate of dVdt=−50 cm³/min (negative because the volume is decreasing). When the thickness of the ice x=5 cm:
R=10+5=15 cm
Substituting into the equation:
−50=4π(15)2⋅dxdt
Step 5: Solve for dxdt
Calculating (15)2=225:
−50=4π⋅225⋅dxdt
−50=900π⋅dxdt
Now, solving for dxdt:
dxdt=−50900π=−118π cm/min
Final Answer
The rate at which the thickness of the ice decreases when the thickness is 5 cm is:
dxdt=−118π cm/min
Let:
- r=10 cm (radius of the iron ball)
- x = thickness of the ice
- Total radius of the sphere with ice = R=r+x=10+x
The volume of the ice can be expressed as the volume of the larger sphere (iron ball + ice) minus the volume of the iron ball:
V=43π(R3)−43π(r3)
Substituting R=10+x and r=10:
V=43π((10+x)3−103)
To find the rate at which the thickness of the ice decreases, we differentiate the volume V with respect to time t:
dVdt=ddt(43π((10+x)3−103))
Using the chain rule:
dVdt=43π⋅3(10+x)2⋅dxdt
This simplifies to:
dVdt=4π(10+x)2⋅dxdt
We know that the ice melts at a rate of dVdt=−50 cm³/min (negative because the volume is decreasing). When the thickness of the ice x=5 cm:
R=10+5=15 cm
Substituting into the equation:
−50=4π(15)2⋅dxdt
Calculating (15)2=225:
−50=4π⋅225⋅dxdt
−50=900π⋅dxdt
Now, solving for dxdt:
dxdt=−50900π=−118π cm/min
The rate at which the thickness of the ice decreases when the thickness is 5 cm is:
dxdt=−118π cm/min
Similar Questions
A spherical iron ball 10cm in radius is coated with a layer of ice of uniform thickness that melts at a rate of 50cm3/m∈ . When the thickness of ice is 5cm, then find the rate at which the thickness of ice decreases.
View SolutionA layer of ice of thickness y is on the surface of a lake. The air is at a constant temperature −θ∘C and the ice water interface is at 0∘C. Show that the rate at which the thickness increases is given by
dydt=KθLρy
where, K is the thermal conductivity of the ice, L the latent heat of fusion and ρ is the density of the ice.View Solution
Knowledge Check
- Question 1 - Select One
A spherical iron ball 10 cm in radius is coated with a layer of ice of uniform thickness that melts at a rate of 50cm3/min. When the thickness of ice is 5 cm, then the rate at which the thickness of ice decreases, is:
A136πcm/minB118πcm/minC154πcm/minD56πcm/min - Question 2 - Select One
A spherical iron ball 10 cm in radius is coated with a layer of ice of unirform thichness that melts at a rate of 50cm3/min. when the thickness of ice is 5 cm, then the rate at which the thickness of ice decreases, is
A154πcm/minB56πcm/minC136πcm/minD118πcm/min - Question 3 - Select One
A spherical iron ball of radius 10cm, coated with a layer of ice of uniform thickness, melts at a rate of 100πcm3/ min.The rate at which the thickness decreases when the thickness of ice is 5 cm, is
A1cm/ minB2cm/minC1376cm/ minD5cm/ min
A spherical ball of radius 10 cm is enclosed by ice of iniform thickness in spherical shape. If ice melts at the rate of 50cm3/min then the rate of decrease of thickness of ice when thickness of ice is 5 cm is
View SolutionA sphere of 10cm radius has a uniform thickness of ice around it. Ice is melting at rate 50cm3/min when thickness is 5cm then rate of change of thickness
View SolutionA spherical balloon in expending. If the radius is increasing at the rate of 2 cm/ min, then the rate at which the volume increases (in cm3/min), when the radius is 5 cm, is
View SolutionIf the side of a cube decreases at the rate of 0.02cm/sec, then, when the side is 10 cm , volume of the cube decreases at the rate of
View SolutionA piece of Ice floats in a vessel with water above which a layer of lighter oil is poured. When ice melts
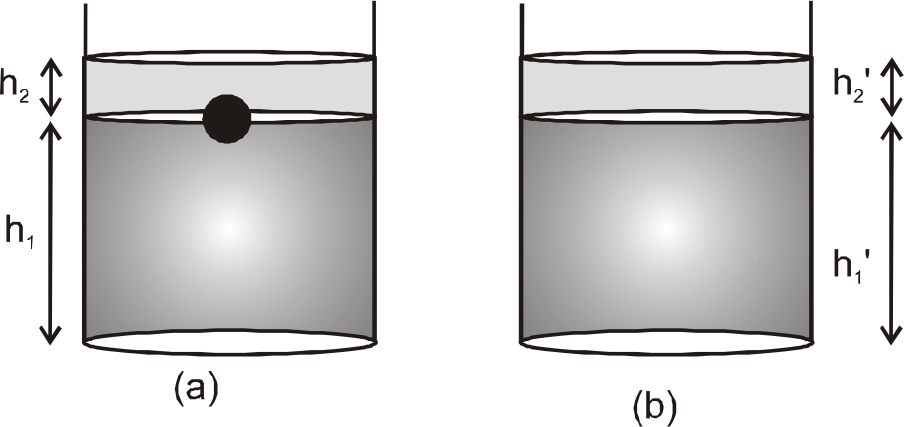
1. The level of oil water interface falls , 2. The level of oil water interface rises
3. The thickness of oil layer decreases , 4. The thickness of oil layer remain same
5. The thickness of oil layer increases , 6. The level of oil-air interface falls
7. The level of oil-air interface remains same , 8. The level of oil-air interface rises
Select the correct alternatives :View Solution

