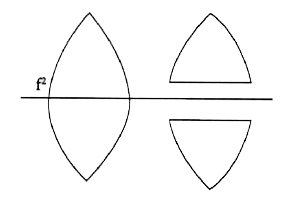
The equiconvex lens has focal length f. If is cut perpendicular to the principal axis passin through optical centre, then focal length of each half is

A

$\frac{f}{2}$

B

2f

C

$\frac{3 f}{2}$

D

f

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

As, for equiconvex lens $R_{1} = R_{2} = R$ ( say )
So, $\frac{1}{f} = (μ_{real} - 1) \frac{2}{R}$ … ( i)
Now, if lens is cut along the line perpendicular to the principal axis as shown in the figure,

The new cut part of the lens has, $R_{1} = R and R_{2} = \infty$
Again by using the lens Maker's formula, focal length of the new part of the lens,
$\frac{1}{f'} = (μ_{real} - 1) [\frac{1}{R} - (- \frac{1}{\infty})]$
$\Rightarrow \frac{1}{f} = (μ_{real} - 1) [\frac{1}{R}] ... (i i)$
So, from the Eqs. (i ) and (ii) , we get
$f' = 2 f$

|

Updated on:21/07/2023

Class 12 PHYSICS MHTCET 2019 PAPER 1

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
AThe focal length of each half becomes $\frac{f}{2}$
BThe focal length of each half becomes 2f
CThe focal length of each half remains f
DThe focal length of each half becomes f4
Question 2 - Select One
If a symmetrical convex lens of focal length 'f is cut into two parts along the principal axis as shown in the figure, the focal length of each part will be:

A $\frac{f}{2}$
B $\frac{f}{4}$
Cf
D $\infty$
Question 3 - Select One

The focal length of the convex lens is
A $+ 10$ cm
B $+ 20 c m$
C $- 10 c m$
D $- 20 c m$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-MHTCET 2019 PAPER 1-PHYSICS

Home
Ask Doubt
Profile