Assertion (A): The following intramolecular aldol reaction occurs.
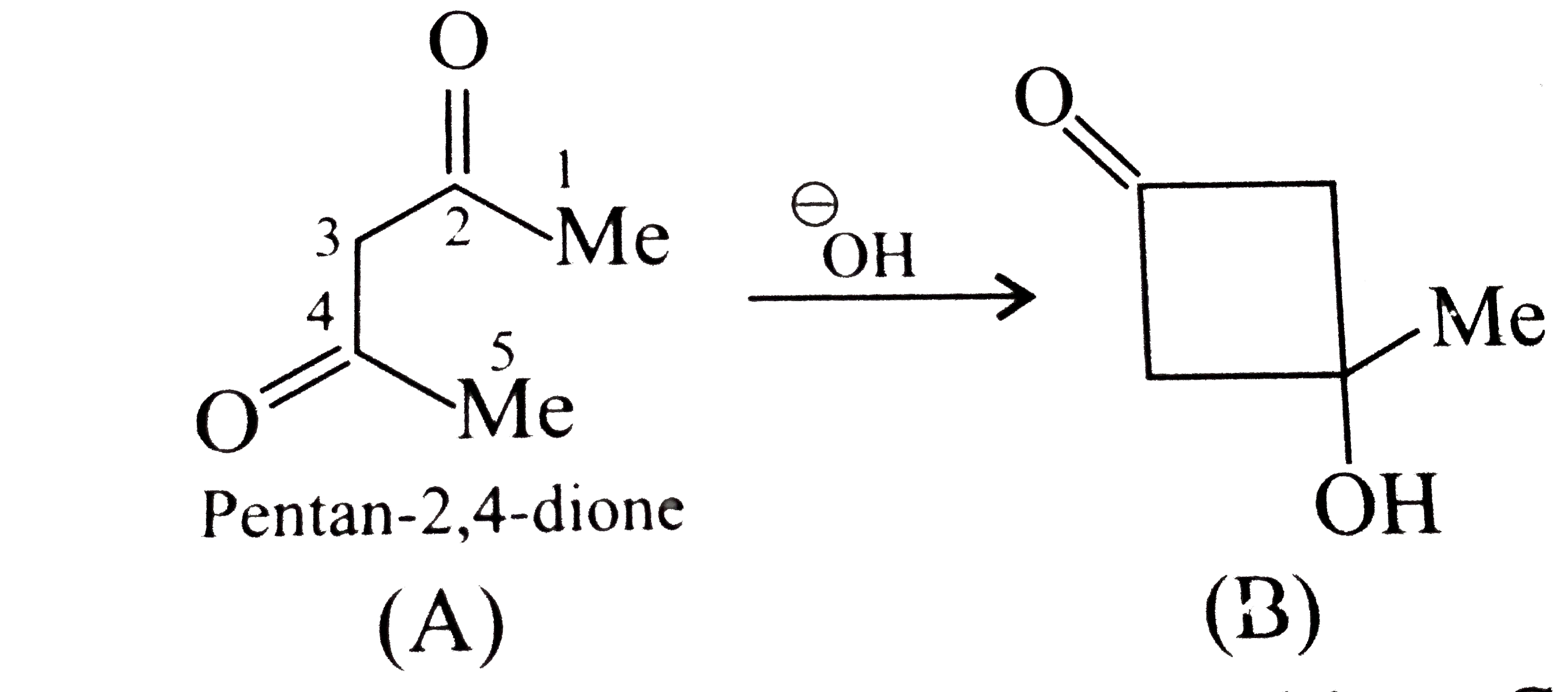
Reason (R ): The carbanion does not add to C-4 because a strained four-membered ring would result.
Both (A) and (R ) true and (R ) is the correct explanation of (A).
Both (A) and (R ) are true but (R ) is not correct explanation of (A).
(A) is true but (R ) is false.
(A) is false but (R ) is true.
The correct Answer is:D
Step by step video, text & image solution for Assertion (A): The following intramolecular aldol reaction occurs. Reason (R ): The carbanion does not add to C-4 because a strained four-membered ring would result. by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESBook:CENGAGE CHEMISTRYChapter:ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESExercise:Archives Objective
Explore 10 Videos
- ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESBook:CENGAGE CHEMISTRYChapter:ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESExercise:Archives Multiple Correct
Explore 8 Videos
- ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESBook:CENGAGE CHEMISTRYChapter:ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESExercise:Exercises Single Correct
Explore 72 Videos
- ALCOHOL,PHENOL AND ETHERSBook:CENGAGE CHEMISTRYChapter:ALCOHOL,PHENOL AND ETHERSExercise:Archives Analytical And Descriptive
Explore 15 Videos
- AMINESBook:CENGAGE CHEMISTRYChapter:AMINESExercise:QUESTION BANK
Explore 1 Video
Similar Questions
Assertion (A): The process of DNA copying does not result in variations.
Reason (R): No biochemical reaction is absolutely reliable
View Solution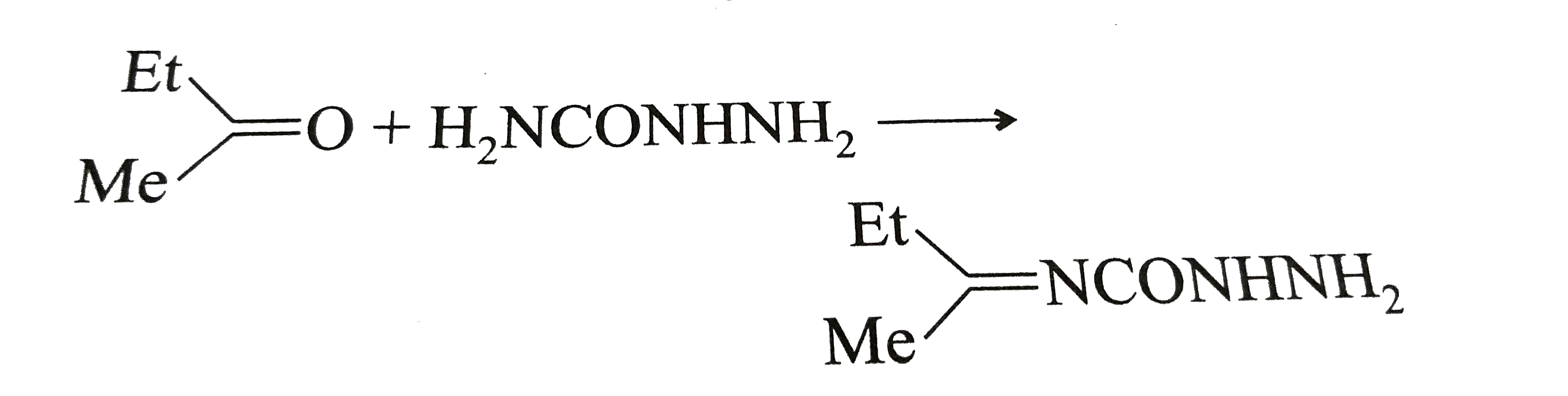
(a) If both the assertion and reason are true and reason is a true explanation of the assertion.
(b) If both the assertion and reason are true but the reason is not the correct explanation of assertion.
(c) If the assertion is true but reason is false.
(d) If assertion is false but reason is true.
Q. Assertion: The following reaction occurs:
Reason: The semicarbazone of (A) (pentan-2-one) exists in two geometrical isomers.
View Solution
Knowledge Check
Assertion (A): The following intramolecular aldol reaction occurs.
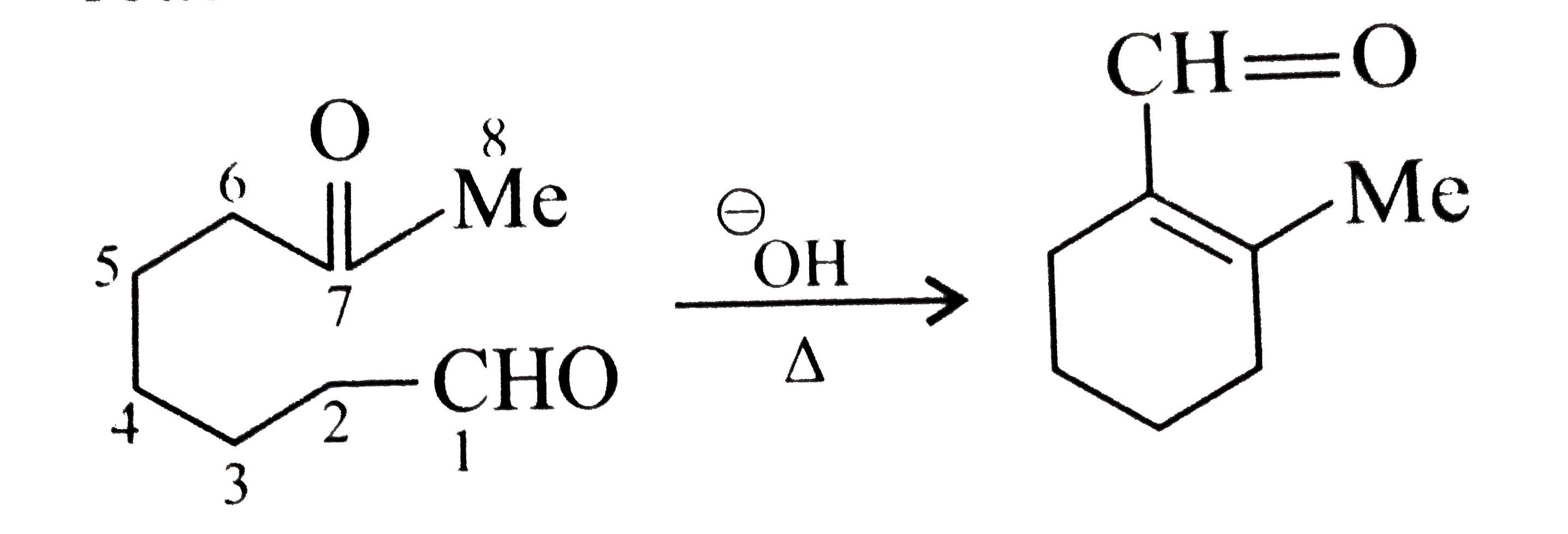
Reason (R ): (CHO) is a better acceptor than (C==O).ABoth (A) and (R ) true and (R ) is the correct explanation of (A).BBoth (A) and (R ) are true but (R ) is not correct explanation of (A).C(A) is true but (R ) is false.D(A) is false but (R ) is true.Assertion (A): The following reaction occurs.
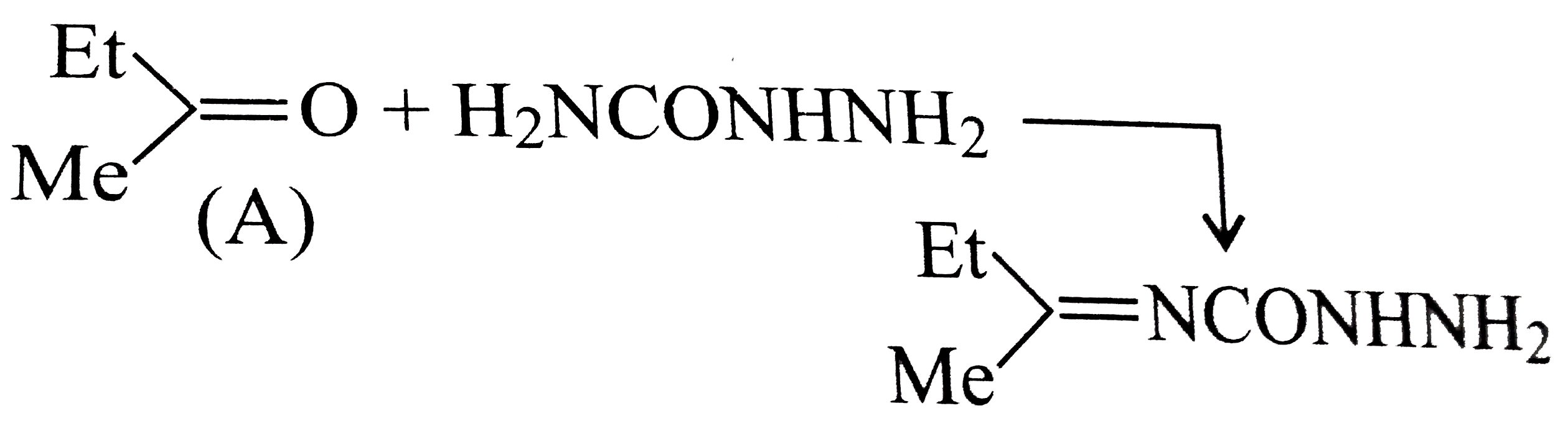
Reason (R ): The semicarbazone of (A) (pentan-2-one) exists in two geometrical isomers.AIf both (A) and (R ) true and (R ) is the correct explanation of (A).BIf both (A) and (R ) are true but (R ) is not correct explanation of (A).CIf (A) is true but (R ) is false.DIf (A) is false but (R ) is true.Assertion (A): The following cross Cannizzaro reaction occurs.
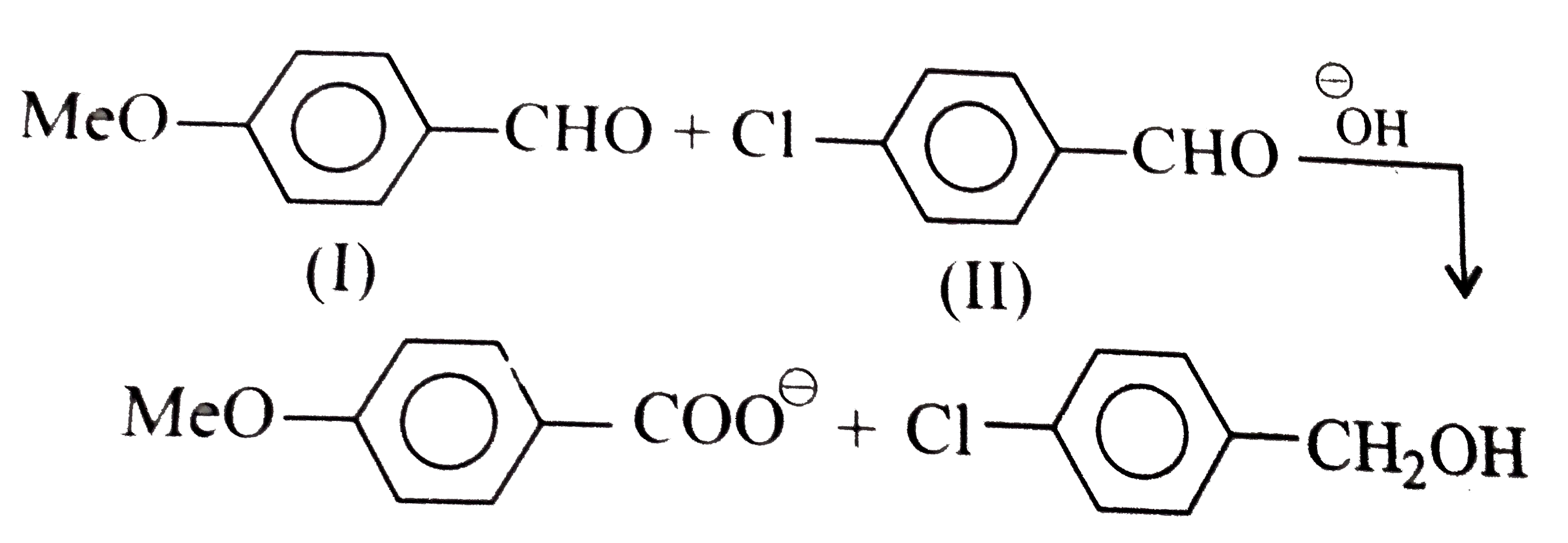
Reason (R ): Rate of reaction is:
Rate = K[Aldehyde(I)][Aldehyde(II)][ΘOH] and bimolecular.AIf both (A) and (R ) true and (R ) is the correct explanation of (A).BIf both (A) and (R ) are true but (R ) is not correct explanation of (A).CIf (A) is true but (R ) is false.DIf (A) is false but (R ) is true.
Assertion (A): The following reaction occurs.
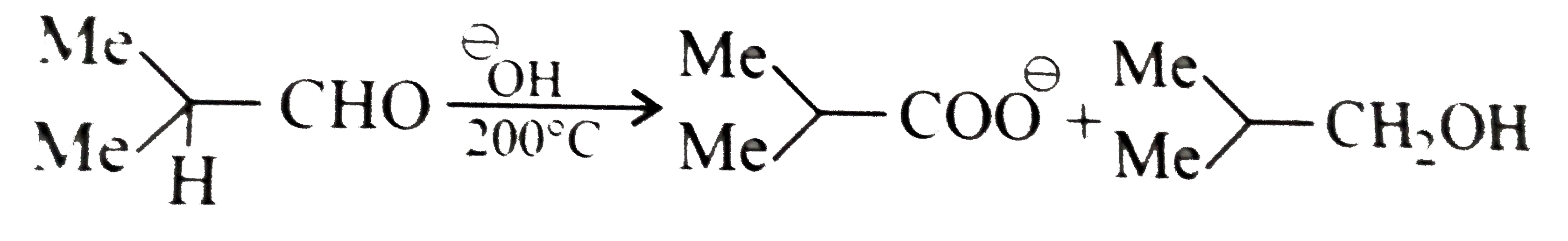
Reason (R ): Undergoes disproportionation reaction since the mobility of α−H atom is arrested by the steric effect of the two bulky methyl groups.
View SolutionAssertion (A) : Nitrobenzene does not undergo Friedel-crafts reaction.
Reason (R) : Nitrogroup in nitrobenzene deactivates the benzene ring.
View SolutionAssertion (A) : Carbon forms covalent compounds buyt lead dorms ionic compounds
Reason (R) : crabon can les foure electrons to forem C4+ ion but lead connot .
View SolutionAssertion : In all C4 plants, photorespiration takes place.
Reason: In C4 plants , respiration does not occur in dark.
View SolutionAssertion (A): Pentan-2-one on reaction with NaHSO3 gives sodium bisulphite adduct product.
Reason (R ): (C=O) group of pentan-3-one is sterically hindered and nucleophile SO2−3 is also of large size, so nucleophilic addition reaction does not occur.
View Solution

