0.218 gm of the acetyl derivative of a polyhydric acohol (molecular mass = 92) requires 0.168 gm of KOH for hydrolysis. Calculate the number of (−−OH) groups in the alcohol.
Let the formula of alcohol is R(OH)n, and the formula of its actyl derivative is R(OCOCH3)n.
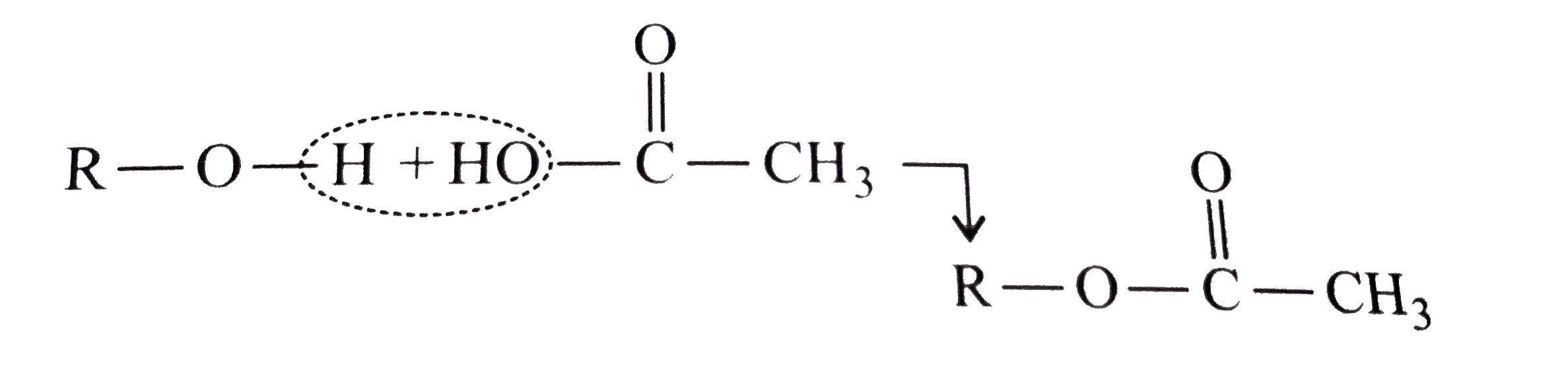
Molecular mass of R(OCOCH3)=(M+42n) M is the molecular mass of alcohol. Molecular mass of (CH3−CO−) group = 43. One H atom is replaced by (OH) group of CH3COOH group. Therefore, molecular mass of R(OCOCH3)
=[M+(43−1)n]
=(M+42n)
R(OCOCH3)n nKOH−−−→ R(OH)n+nCH3COOH
Molecular mass of nKOH=56n
0.218 gm of acteyl derivative requires
=0.168(M+42n)0.218=56n
On solving, we get n = 3
[Use the formula: w(M+42n)W=56n w = Weight of KOH, W = weight of acetyl derivative, M = Molecular mass of alcohol, n - number of (−OH) groups]
Topper's Solved these Questions
- ALCOHOL,PHENOL AND ETHERSBOOK - CENGAGE CHEMISTRYCHAPTER - ALCOHOL,PHENOL AND ETHERSEXERCISE - Solved Examples
17 Videos
- ALCOHOL,PHENOL AND ETHERSBOOK - CENGAGE CHEMISTRYCHAPTER - ALCOHOL,PHENOL AND ETHERSEXERCISE - Exercises Subjective
25 Videos
- ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESBOOK - CENGAGE CHEMISTRYCHAPTER - ALIPHATIC AND AROMATIC ALDEHYDES AND KETONESEXERCISE - Archives Subjective
29 Videos
Similar Questions
0.436g of acetyl derivative of a polyhydric alcohol (molecular mass =92) required 0.336g KOH for hydrolysis. Calculate the number of hydroxy gropus in the alcohol.
View SolutionA polyhydroxy alcohol having molecular weight =168. On acetylation the molecular weight increases to 294. Determine the number of -OH groups present in the alcohol.
View Solution
Knowledge Check
In Zeisel's method for the detrmination of methoxyl groups, a sample of 2.68 gm of a compound (A) gave 14.08 gm of AgI. If the molecular weight of compound (A) is 134, the number of (−−OH3) group(s) in the compound (A) is:
A1B2C3D4
Explain the following:
(a) In sodium fusion test, why excess of sodium is taken?
(b) acetals give positive test with 2,4 dinitrophenylhydrazine..
(c) A polyhydroxy alcohol has the molecualr weight of 168. On acetylation, the molecular weight increases to 294. Determine the number of (−OH) groups present in the alcohol.
(d) Chlorobenzene when treated with enhanilic AhNO3 does not give white precipate.
View SolutionHaemoglobin contains 0.25 % iron by mass. The molecular mass of haemoglobin is 89600. Calculate the number of iron atoms per molecule of haemoglobin.
View SolutionHaemoglobin contains 0.25% iron by mass. The molecular mass of haemoglobin is 89600. calculate the number of iron atoms per molecule of haemoglobin.
View Solution4.6 g of a polydric alcohol was treated with an excess of methyl magnesium bromide to produce 3.36 liter of CH4 at STP. Calculate number of -OH(molecular weight of alcohol = 92)
View Solution3.8gm of a tribasic carboxylic acid derivative of a saturated hydrocarbon required 100 ml of 0.6MNaOH solution to reach equivalence point. Calculate molar mass of tribasic carboxylic acid derivative of saturated hydrocarbon.
View SolutionThe number of alkoxy groups in an organic compound, A(OR)x, may be determined by the sequential reactions:
A(OR)x+xHI→A(OH)x+xRI
RI+Ag++H2O→ROH+AgI(s)+H+ When 4.8 gm of the organic compound, A(OR)x, (molar mass=240 gm//mol) is treated as above, 9.4 gm Agl is precipitated. The number of alkoxy groups in the compound is:
View Solution0.075 g of a monobasic acid required 10 mL of N/12NaOH solution for complete neutralisation. Calculate the molecular mass of the acid
View Solution
