One the basis of $V B T$ answer the following complex ions
(i) ${[T i {(b p y)}_{3}]}_{3}^{Θ}$
(b) ${[V {(H_{2} O)}_{6}]}_{6}^{3 +}$
(ii) ${[V {(H_{2} O)}_{6}]}_{6}^{3 +}$
(III) ${[M n {(C N)}_{6}]}_{6}^{4 -}$
$[M n {(C N)}_{6})]^{3 -}$
(V) ${[I r {(N H_{3})}_{6}]}_{6}^{3 +}$ .
Type of hybridisation involed
(b) Type of inner or outer orbital octahedral complex
(c ) Magnetic behaviour and $μ_{s π n}$ value .

Video Solution

Text Solution

Verified by Experts

bpy or dipy is a strong field neutral bidentage ligand

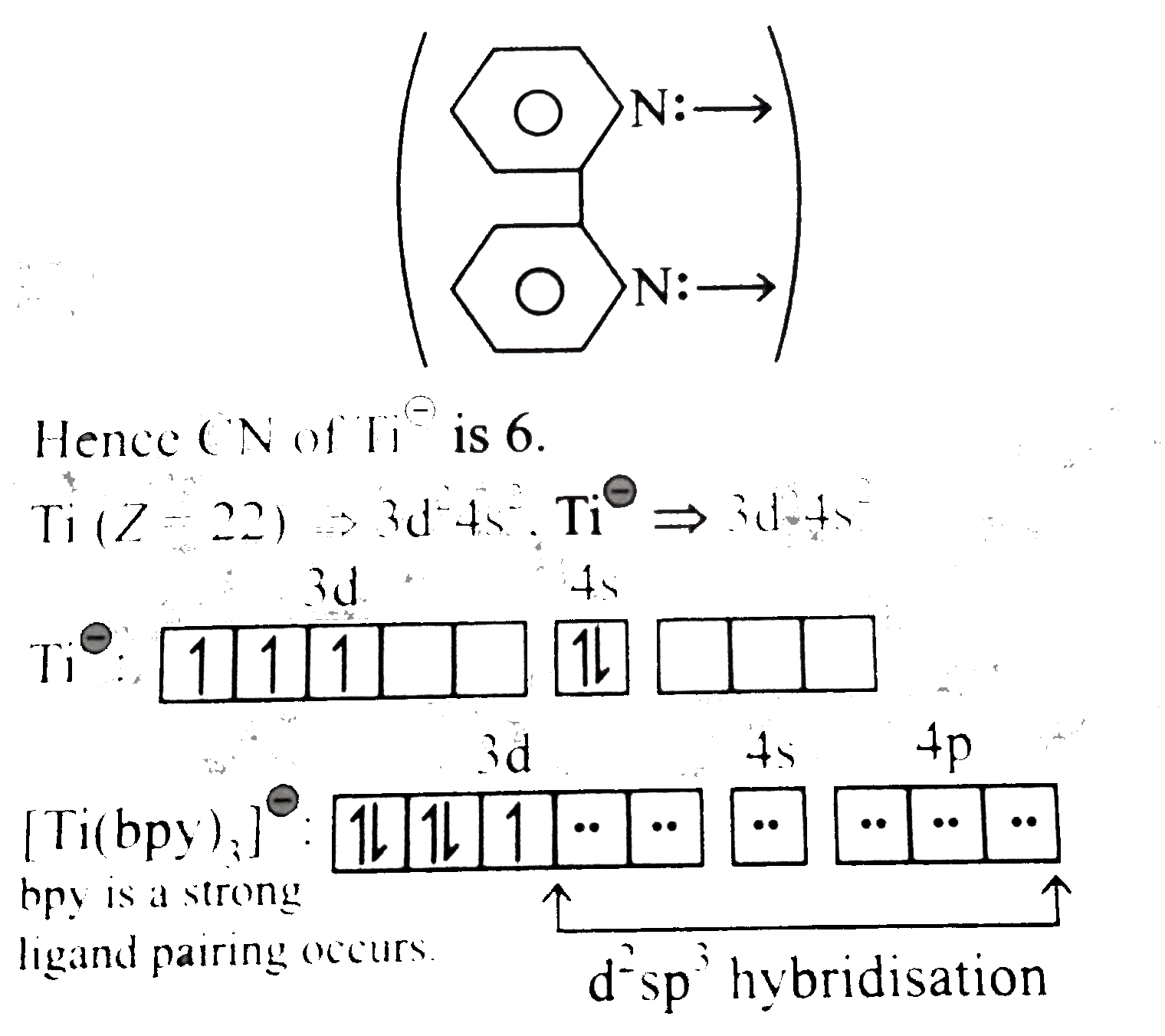
(a) $d^{2} s p^{3}$ hybridisation with $O H$ shape
(b) Inner orbital complex
( c) Paramagnetic $n = 1$
$μ_{spin} = \sqrt{3} B M = 1.732 B M$
(II) $[V {(H_{2}_(o)]}_{2}^{3 +}$
$V (Z = 23) \Rightarrow 3 d^{3} 4 s^{2}, V^{3 +} = 3 d^{2} 4 s^{0}$
$C N^{Θ}$ is a strong field ligand so pairing occurs

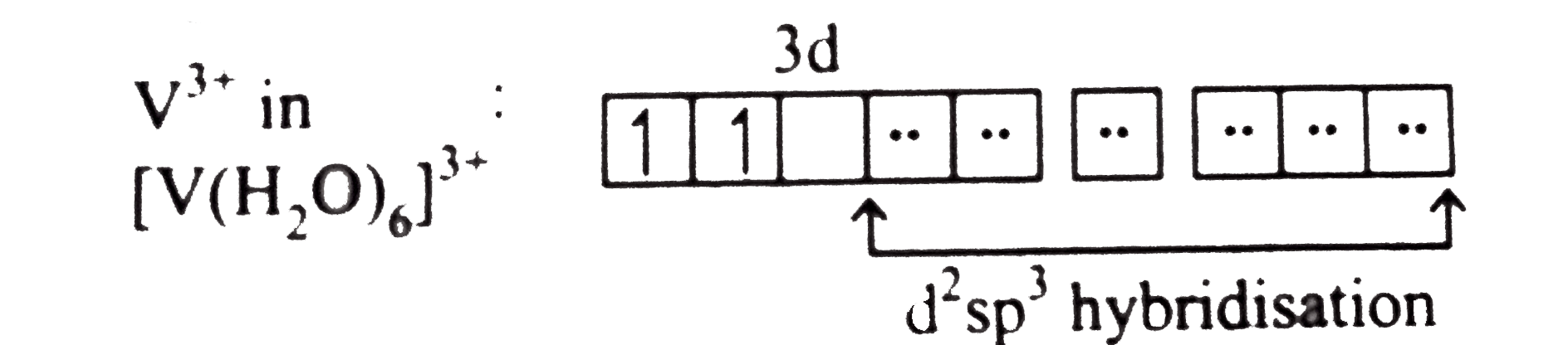
$d^{2} s p^{3}$ hybridisation with $O H$ shape
(b) Inner orbital complex
(c ) Paramagnetic , $n = 2$
(d) $μ (spin) = \sqrt{8} B M = 2.828 B M$
(III) ${[M n {(C N)}_{6}]}_{6}^{4 -}$
$M n (Z = 25) \Rightarrow 3 d^{5} 4 s^{2}, M n^{2 +} = 3 d^{54 s^{0}}$
$C N^{Θ}$ is a strong field ligand so pairing occurs

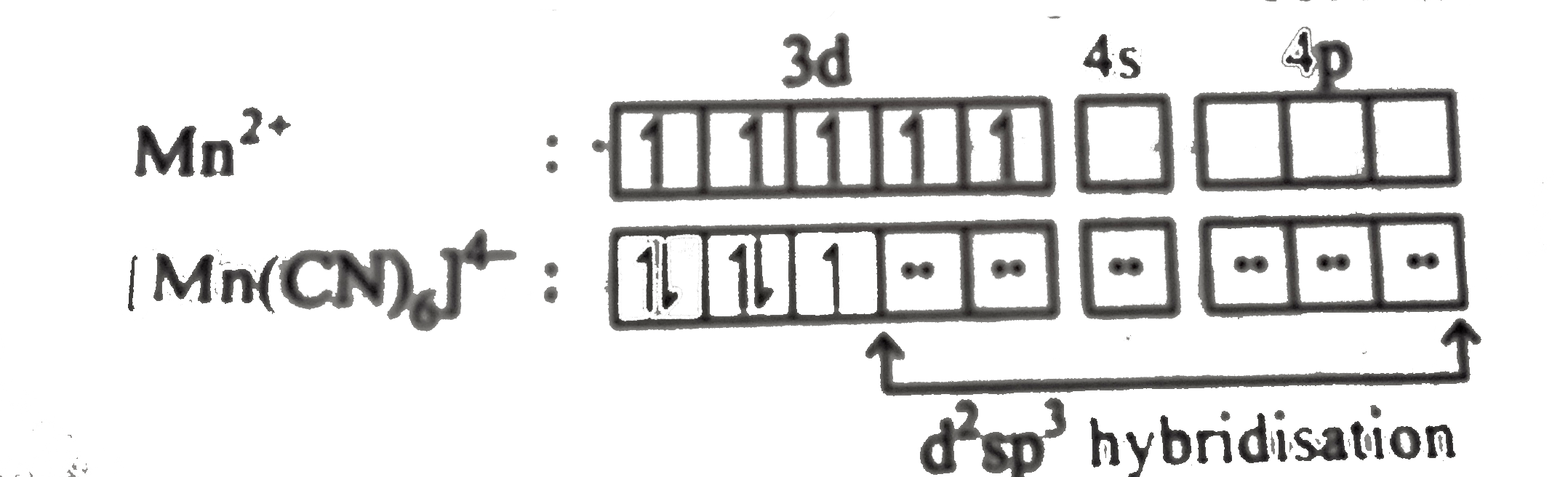
(a) $d^{2} s p^{3}$ hybridisation with $O H$ shape
(b) Inner orbital complex
(c) Paramagnetic $n = 1$
(d) $μ_{s π n} = \sqrt{3} B M = 1.732 B M$
(IV) ${[M n {(C N)}_{6}]}_{6}^{3 -}$
$M n (Z = 25) \Rightarrow 3 d^{5} 4 s^{2}, M n^{3 +} = 3 d^{4} 4 s^{0}$
$C N^{Θ}$ is a strong field ligand so only one pairing occurs

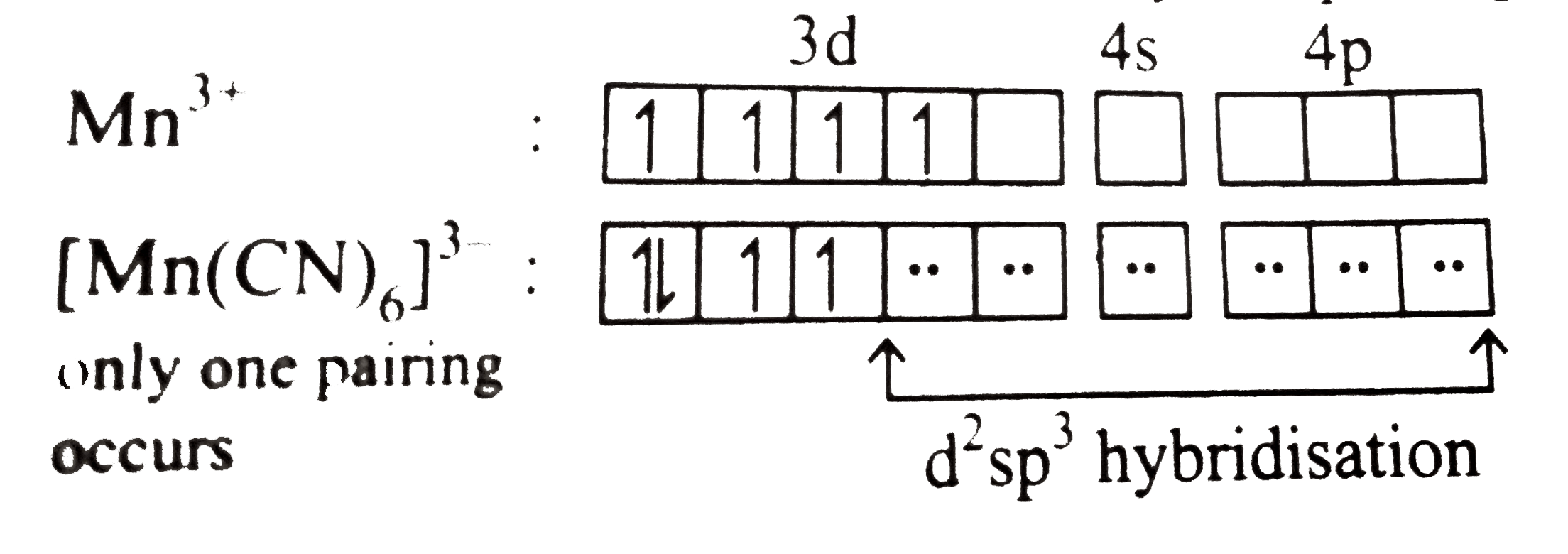
(a) $d^{2} s p^{3}$ hybridisation with $O H$ shape
(b) Inner orbital complex
(c ) Paramagnetic $n = 2$
(d) $μ_{spin} = \sqrt{8} B M = 2.828 B M$
(V) ${[I r {(N H_{3})}_{6}]}_{6}^{3 +}$
ir(Z=7)implies5d^(7) 6s^(2), Ir^(3+) = 5d^(6) 6s^(0) $ (a)$ d^(2)sp^(3) $h y b r s a t i o n (b) I \cap e r or b i t a l c o m p \leq x (c) D i a m a g \neq t i c$ mu_("spin")=0 .

Updated on:21/07/2023