One the basic of CFT predict the geometry of the compund K3[Mn(CN)6] Also calculate the value of μsπn only of the compund .
Ink3[Mn(CN)6],[Mn(CN)6]3− is the complex ion In [Mn(CN)6]3− the oxidation state of central metal ion Mnis+3(Mn=3d54s2,Mn3+=3d4)
CN of Mn in [Mn(CN)6]3− the oxidation state of central metal ion
Mn is +3(Mn=3d54s2,Mn3+=3d4)
CN of Mn in [Mn(CN)6]3− is 6 hence it is an octahedral complex CNΘ ion is a strong field ligand therefore [Mn(CN)6]3− is low spin octahedral complex and hence Mn3+ ion (Mn(CN)6]3−) is
Splitting of d-orbitals in octahedral geometry with n=2
μsπn=√2(2+2)=2.83BM .
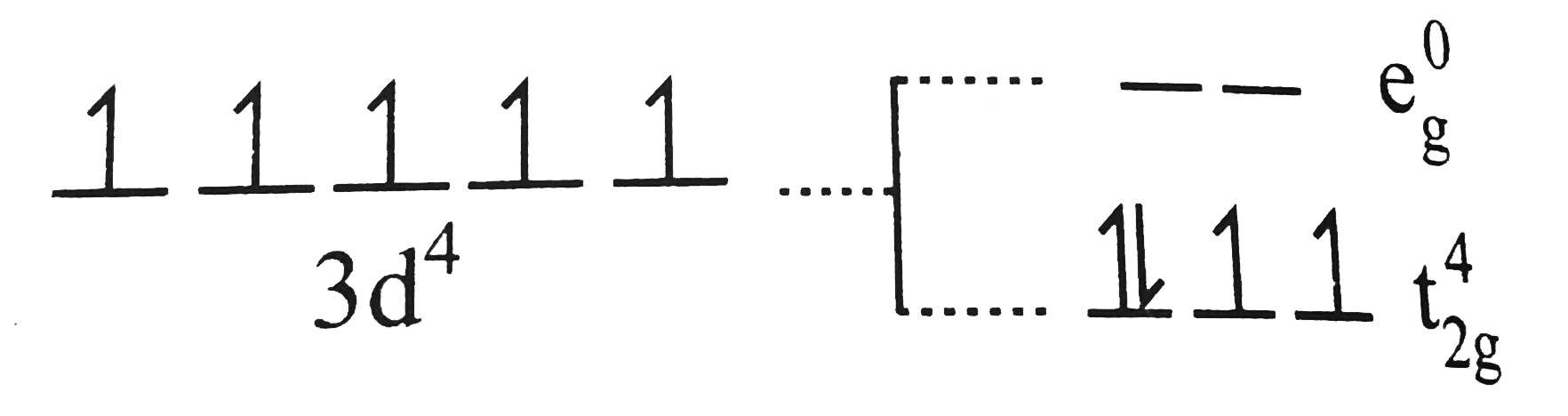
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Ex 7.1 Subjective (Terminology)
5 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Ex 7.1 Subjective (Effective Atomic Number (Ean))
3 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Archives Subjective
23 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRYCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective
29 Videos
Similar Questions
On the basic VBT answer the following questions for the 4-coordinated complex compounds
(a) [CoBr4]2−, (b) [Zn(CN)4]2−, (c ) [MnCI4]2−
(i) What is the oxidation state of the central metal atom//ion?
(ii) What type of hybridisation is involved?
(iii) What is the geometry and magnetic behaviour of the complex ion/compound
(iv) Calculate the value of μsπn only .
View Solution(i) Predict the geometry of [NiCN4]2− (ii) Calculate the spin only magnetic moment of [Cu(NH3)4]2+ ion.
View Solution
Knowledge Check
The complex K3[Fe(CN)6] should have a spin only magentic of
A√8BMB2√5BMC√3BMD√6BMThe spin magnetic moment of iron in K3[Fe(CN)6]
A√3BMB√5BMC√15BMD√24BM27.6gK2CO3 was treated by a series of reagents so as to convent all of its carbon to K2Zn3[Fe(CN)6]2 Calculate the weight of the product [mol.wt. of K2CO3=138 and mol. Wt. of K2Zn3[Fe(CN)6]2=698] .
A11.6gB116gC1.16gD0.116g
27.6 g of K2CO3 was treated by a series of reagents so as to convert all of its carbon to K2Zn3[Fe(CN)6]2 Calculate the weight of the product.
View Solution27.6gK2CO3 was treated by a series of reagents so as to convent all of its carbon to K2Zn3[Fe(CN)6]2 Calculate the weight of the product [mol.wt. of K2CO3=138 and mol. Wt. of K2Zn3[Fe(CN)6]2=698] .
View SolutionCalculate the magnetic moment (spin only) of manganese in K4[Mn(NCS)6].
View SolutionMagnetic moment value of [Mn(CN)6]3− ion in 2.8BM Predict the type of hybridisation and geometry of the ion .
View SolutionVan 't hoff factor of centimolal solution of K3[Fe(CN)6] is 3.333 calculate the per cent dissociation of K3[Fe(CN)6]
View Solution
