Let a,b, and c be three real numbers satistying $[a, b, c] [\begin{matrix} 1 & 9 & 7 \\ 8 & 2 & 7 \\ 7 & 3 & 7 \end{matrix}] = [0, 0, 0]$ Let b=6, with a and c satisfying (E). If alpha and beta are the roots of the quadratic equation $a x^{2} + b x + c = 0 t h e n \sum_{n = 0}^{\infty} {(\frac{1}{α} + \frac{1}{β})}^{n}$ is (A) 6 (B) 7 (C) $\frac{6}{7}$ (D) oo

A

6

B

3

C

$\frac{6}{7}$

D

$\infty$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$∵ b = 6,$ with a and c satisgying ( E)
$∴ a + 48 + 7 c = 0, 9 a + 12 + 3 c = 0, a + 6 + c = 0$
we get $a = 1, c - 7$
Given, $α, β$ are the roots of $a x^{2} + b x + c = 0$
$∴ α + β = - \frac{b}{a} = - 6,$
$α β = \frac{c}{a} = - 7$
Now, $\frac{1}{α} + \frac{1}{β} = \frac{α + β}{α β} = \frac{- 6}{- 7} = \frac{6}{7}$
$∴ \sum_{n = 0}^{\infty} {(\frac{1}{α} + \frac{1}{β})}^{n} = \sum_{n = 0}^{\infty} {(\frac{6}{7})}^{n}$
$= 1 + (\frac{6}{7}) + {(\frac{6}{7})}^{2} + ... \infty$
$\frac{1}{1 - 6 / 7} = 7$

|

Updated on:21/07/2023

Class 12 MATHS MATRICES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $b = 6$ with a and c satisfying (1). If $α$ and $β$ are the roots of the quadeatic equation $a x^{2} + b x + c = 0, t h e n$ is
A6
B7
C $\frac{6}{7}$
D $\infty$
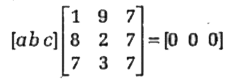Question 2 - Select One
If $α$ and $β$ are the roots of the , quadratic equation , $a x^{2} + b x + c = 0$ ,with $α < β$ ,then for $x < α$ (or) $x > β$ , $a x^{2} + b x + c$ and $a$ have ,
(A) Opposite sign
(B) Positive sign
(C) same sign
(D) none of these
Arational numbers
Breal and negative
Cnegative real parts
Dnone of these
Question 3 - Select One
If $α$ and $β$ are the roots of the equation $a x^{2} + b x + c = 0$ , then $\frac{α}{α β + b} + \frac{β}{a α + b}$ is equal to
A $\frac{2}{a}$
B $\frac{2}{b}$
C $\frac{2}{c}$
D $- \frac{2}{a}$

ARIHANT MATHS-MATRICES -Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile