If the sides of a angled triangle are in A.P then the sines of the acute angles are
A
35,45
B
√3,13
C
√√5−12,√√5+12
D
√32,12
Video Solution
Text Solution
The correct Answer is:A
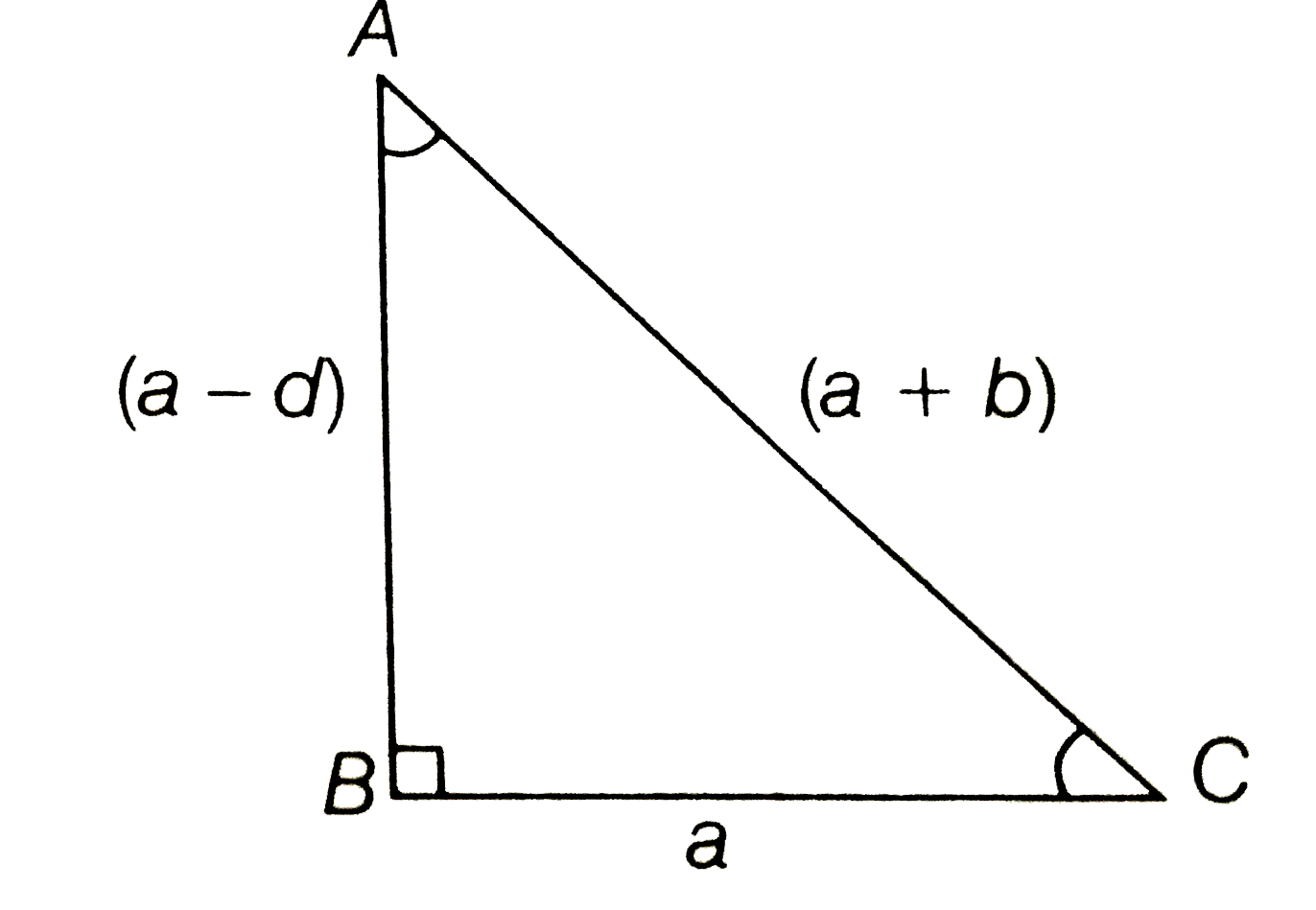
Let the sides of right angled triangle be
(a−d),(a+d)(a>d).
By Pythagoras theorem,
(a+d)2=a2+(a−d)2
a2+d2+2ad=a2+a2+d2−2ad
a2=4ad
a=4d' [since ane 0]……(i)
According ti the question, sinA=a(a+d)=4d5d=45
sinC=a−da+d=3d5d=35.
|
Topper's Solved these Questions
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise (More Than One Correct Option Type Questions)
Explore 15 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise (Passage Based Questions)
Explore 24 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise For Session 7
Explore 7 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHSChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 12 Videos
Similar Questions
Knowledge Check
If the sides of a right angled triangle are in A.P. then the sines of the acute angles are
A35,45B√3,13C√√5−12,√√5+12D√32,12If the side of a right-angled triangled are in A.P., then tangents of its acute angled are
A√√3+12,√√3−12B√√5+12,√√3−12C√3,1/√3D3/4,4/3If the altitudes of a triangle are in A.P,then the sides of the triangle are in
AA.P.BG.P.CH.P.Dnone of these
The sides of a right angled triangle arein A.P., then they are in the ratio
View SolutionIf the sides of a triangle are in A.P., then the cotangent of its half the angles will be in
View SolutionStatement- 1: If the sines of the angles of a triangle are in A.P., then the altitudes ef the triangle are also in A.P.
Statement-2: Twice the area of a triangle is equal to the product of the lengths of a side and the altitude on it.
View SolutionIf the sides of a right angled triangle are in A.P., then Rr=
View SolutionIf the sides of a triangle are in A.P. and the greatest angle of the triangle exceeds the least by 90∘, then sine of the third angle is
View Solution

