The following equations represent progressive transverse waves
z1=Acos(ωt−kx)
z2=Acos(ωt+kx)
z3=Acos(ωt+ky)
z4=Acos(2ωt−2ky)
A stationary wave will be formed by superposing
z1andz2
z1andz4
z2andz3
z3andz4
The correct Answer is:A
To determine which two waves can be superimposed to create a stationary wave, we need to analyze the given wave equations.
1. Identify the wave equations:
- z1=Acos(ωt−kx)
- z2=Acos(ωt+kx)
- z3=Acos(ωt+ky)
- z4=Acos(2ωt−2ky)
2. Check the conditions for forming a stationary wave:
- For two waves to form a stationary wave, they must have the same frequency and travel in opposite directions. The general form of a stationary wave can be expressed as the superposition of two waves traveling in opposite directions.
3. Examine pairs of waves:
- Pair z1 and z2:
- Both have the same angular frequency ω.
- z1 travels in the positive x-direction and z2 travels in the negative x-direction.
- Since they meet the criteria (same frequency and opposite directions), they can form a stationary wave.
- Pair z1 and z4:
- z1 has frequency ω and z4 has frequency 2ω.
- Since the frequencies are different, they cannot form a stationary wave.
- Pair z2 and z3:
- z2 travels in the x-direction and z3 travels in the y-direction.
- Since they are in different directions, they cannot form a stationary wave.
- Pair z3 and z4:
- z3 has frequency ω and z4 has frequency 2ω.
- Since the frequencies are different, they cannot form a stationary wave.
4. Conclusion:
- The only pair of waves that can be superimposed to create a stationary wave is z1 and z2.
Final Answer:
The stationary wave will be formed by superposing z1 and z2.
- z1=Acos(ωt−kx)
- z2=Acos(ωt+kx)
- z3=Acos(ωt+ky)
- z4=Acos(2ωt−2ky)
- For two waves to form a stationary wave, they must have the same frequency and travel in opposite directions. The general form of a stationary wave can be expressed as the superposition of two waves traveling in opposite directions.
- Pair z1 and z2:
- Both have the same angular frequency ω.
- z1 travels in the positive x-direction and z2 travels in the negative x-direction.
- Since they meet the criteria (same frequency and opposite directions), they can form a stationary wave.
- z1 has frequency ω and z4 has frequency 2ω.
- Since the frequencies are different, they cannot form a stationary wave.
- z2 travels in the x-direction and z3 travels in the y-direction.
- Since they are in different directions, they cannot form a stationary wave.
- z3 has frequency ω and z4 has frequency 2ω.
- Since the frequencies are different, they cannot form a stationary wave.
- The only pair of waves that can be superimposed to create a stationary wave is z1 and z2.
The stationary wave will be formed by superposing z1 and z2.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Multiple
Explore 26 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Assertion - Reasoning
Explore 6 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Subjective
Explore 24 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
The following equations represent transverse waves :
z1=Acos(kx−ωt),
z2=Acos(kx+ωt), z3=Acos(ky−ωt)
Identify the combineation (s) of the waves which will produce (i) standing wave(s), (ii) awave travelling in the direction making an angle of 45∘ degrees with the positive x and positive y axes. In each case, find the positions at which the resultant is always zero.
View SolutionIf i1=3sinωt and i2=6cosωt, then i3 is
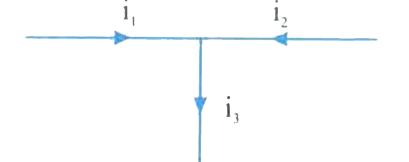
View Solution
Knowledge Check
If i1=3sinωtand(i2)=4cosωt, then (i3) is
 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5sin(ωt+35∘)Three transverse waves are represented by
y1=Acos(kx−ωt)
y2=Acos(kx+ωt)
y3=Acos(ky−ωt)
The combination of waves which can produce stationary waves isAy1andy2By2andy3Cy1andy3Dy1,y2andy3Wave equations of two particles are given by y1=asin(ωt−kx),y2=asin(kx+ωt), then
AThey are moving in opposite directionBPhase between them is 90∘CPhase between them is 180∘DPhase between them is 0∘
y1=4sin(ωt + kx), y2 = -4 cos(ωt + kx), the phase difference is
View SolutionThe r.m.s. value of I=I1sinωt+I2cosωt is
View SolutionThe r.m.s. value of I=I1sinωt+I2cosωt is
View SolutionWhich two of the given transverse waves will give stationary wave when get superimposed?
z1=acos(kx−ωt) (A)
z2=acos(kx+ωt) (B)
z3=acos(ky−ωt) (C)
View SolutionThe ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
View Solution

