A closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]
![A closed orgain pipe of length l(0) is resonating in 5^(th) harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =v(s) Young's modulus for the rod Y and density rho]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIT_JEE_PHY_GMP_ASS_E01_027_Q01.png)
The correct Answer is:125l0vs√yρ
For section AB
l=(2n−1)λ4,wheren=1,2,3,…
f1=vλ=(2n−1)v4l
For section BC
2l=mλ2,wherem=1,2,3,…
f2=vm4l
from (3)+(4)f1=f2
(2n−1)4l=mv4l
n=m+12
m=1,n=1 for fundamental , m=3,n=2
first overtone f2=mv4l=3v4l
Given that f=f2
5vs4l0=3v4l
l=3vl05vs
Therefore , length of the rod =4l=125l0vs√Yρ
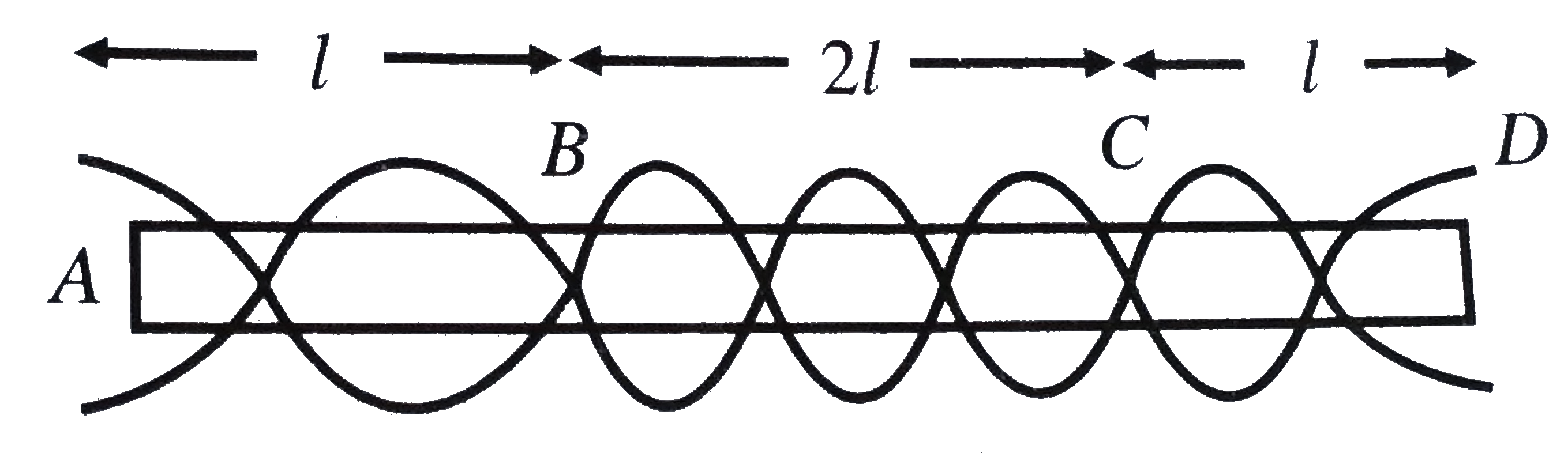
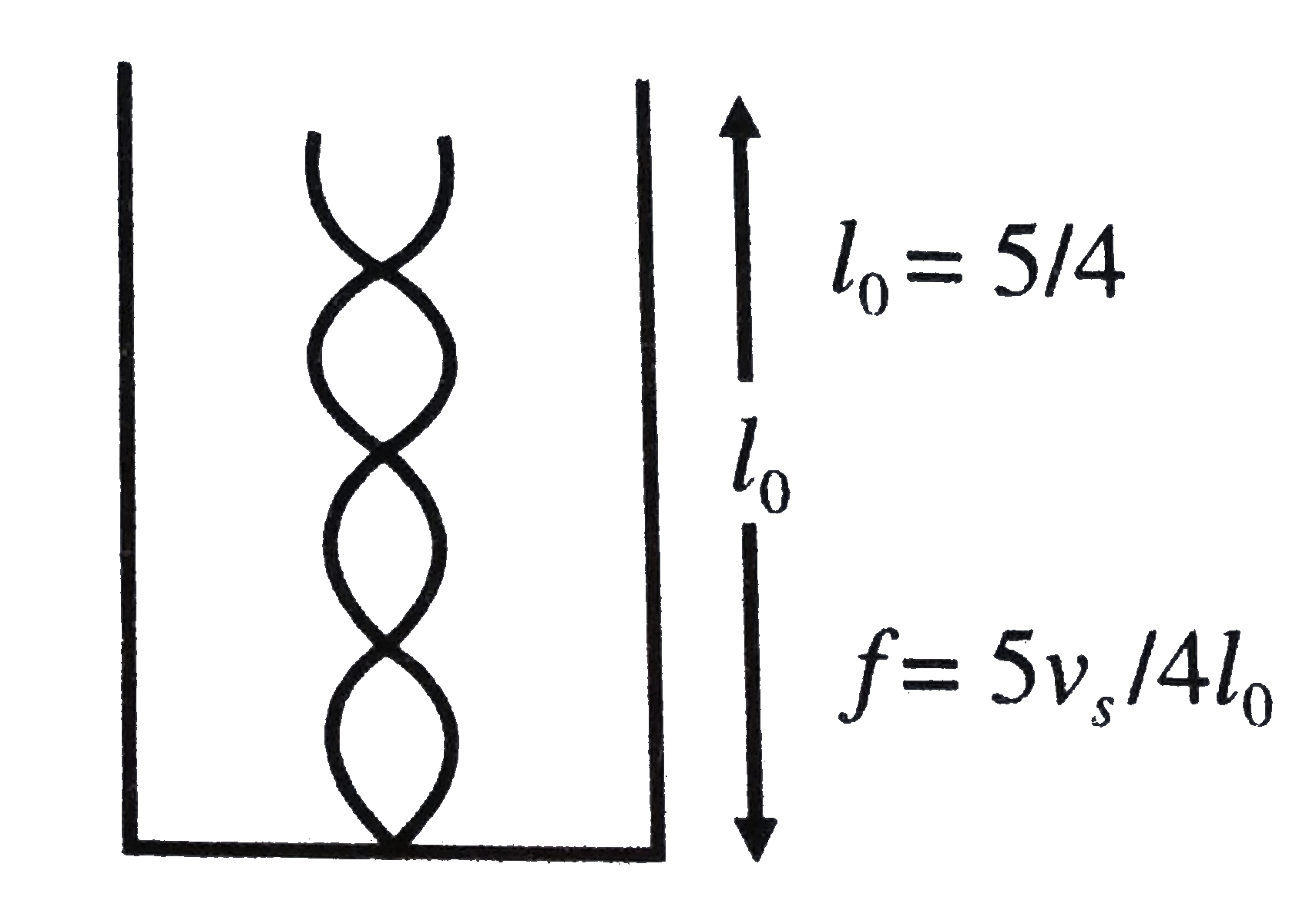
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Single Correct
Explore 144 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Multiple
Explore 26 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Exercise 7.2
Explore 32 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
A rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
View SolutionA rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View Solution
Knowledge Check
A closed organ pipe has length L. The air in it is vibrating in third overtone with maximum amplitude. The amplitude at distanceL7 from closed of the pipe is
A0BaCa2DDate insufficientA uniform rod of length L, has a mass per unit length λ and area of cross section A. The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
A3λgL2AlBλgL22AlC2λgLAlDλgL2AlA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
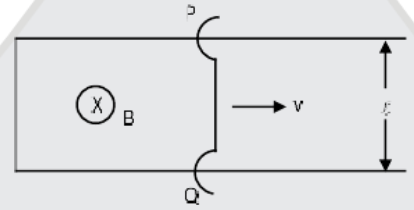 A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
View SolutionIf Young's modulus of the material of a rod is Y and density is ρ then time taken by sound wave to travel l length from bottom is
View SolutionA closed organ pipe has length l. The air in it is vibrating in 3rd overtone with a maximum amplitude of A. Find the amplitude at a distance of l/4 from closed end of the pipe
View Solution

