Question

A pulse moving to the right along the x-axis is represented by the wave function
where x and y are measured in cedntimetres and t is measured in seconds. Find expression for the wave function at $t=0,t=1.0s,\text{and}t=2.0s$ and plote the shape of pulse at these lines.

Explanation

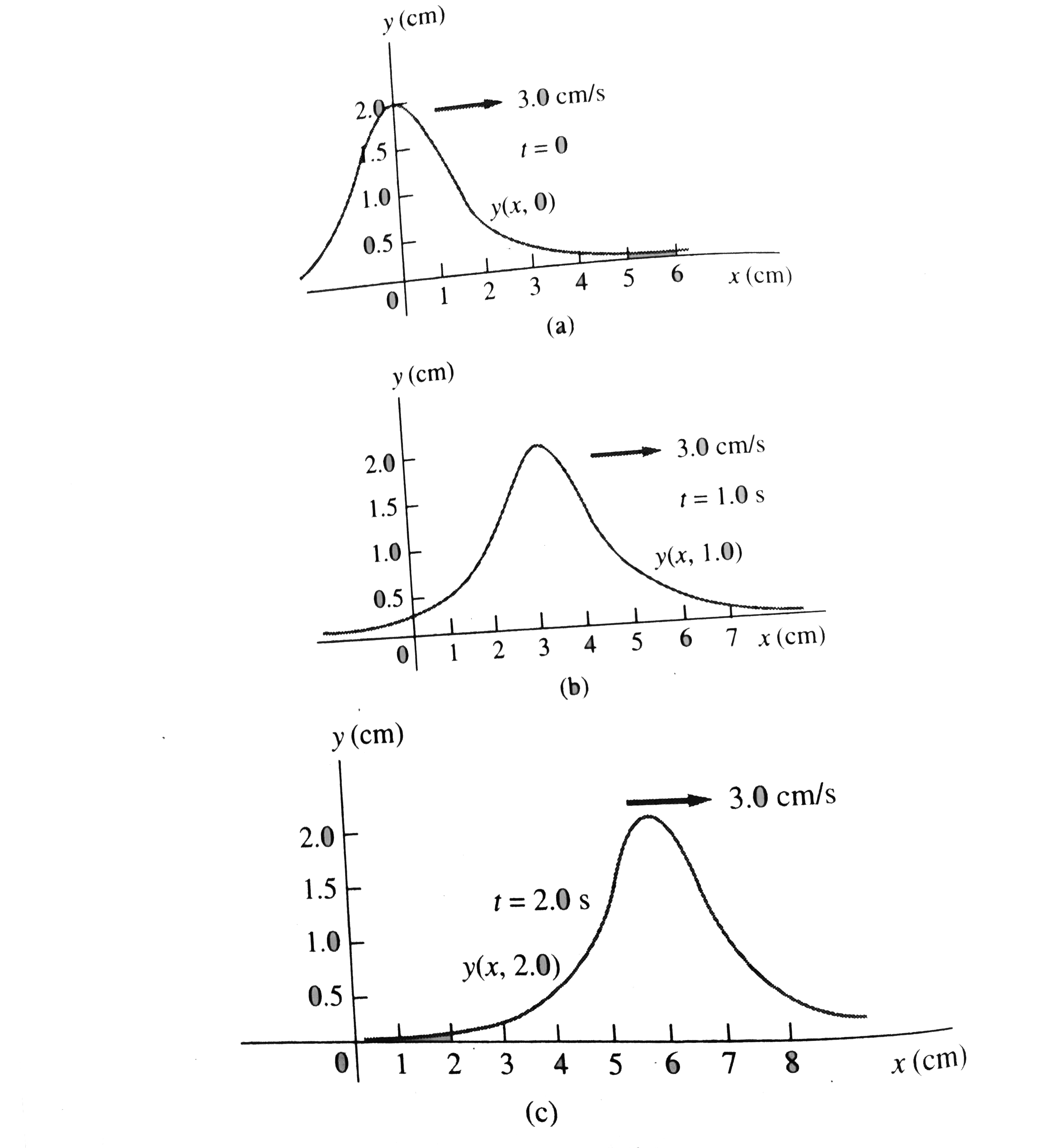
shows the pulse represented by this wave function at t=0. imagine this pulse moving to the right and maintaining its shape as suggested by (b) and (c ).

we categorize this example as a relatively simple analysis problem in which we interpret the mathmatical representation of a pulse.
The wave function is of the form `y=f(x-vt)`. Inspection of the expression for y(x,t) reveals that the wave speed is `v=3.0 cm//s`Furthermore, by letting `x-3.0t=0`, we find that the maximum value of y given by`A=2.0 cm`.
write the wave function expression at `t=0:`
`y(x,0)=(2)/(x^(2)+1)`
write the wave function expression at `t=2.0 s:`
`y(x,1.0)=(2)/(x-3.0)^(2)+1)`
write the wave function expression at `t=2.0 s:`
`y(x,2.0)=(2)/((X-6.0)^(2)+1)`
for each of these expressions we can have various values of x and plot the wave function. this procedure yields the wave function shown in the three parts of ,
these snapshots show that the pulses move to the right without changing its shape and that it has a constant speed of `3.0 cm//s`.
What if the wave function were
`y(x,t)=(4)/(x+3.0t)^(2)+1)`
How would that change the situation?
Answer: One new feature in this expression is the puls sign in the denominator rather than the minus sign. The new expression represents a pulse with the same shape as that in the previous figure, but moving to the left as time progress. Another new feature here is the numerator `4` rather than `2`. Therefore, the new expression represents a pulse with twice the height of that in figure.