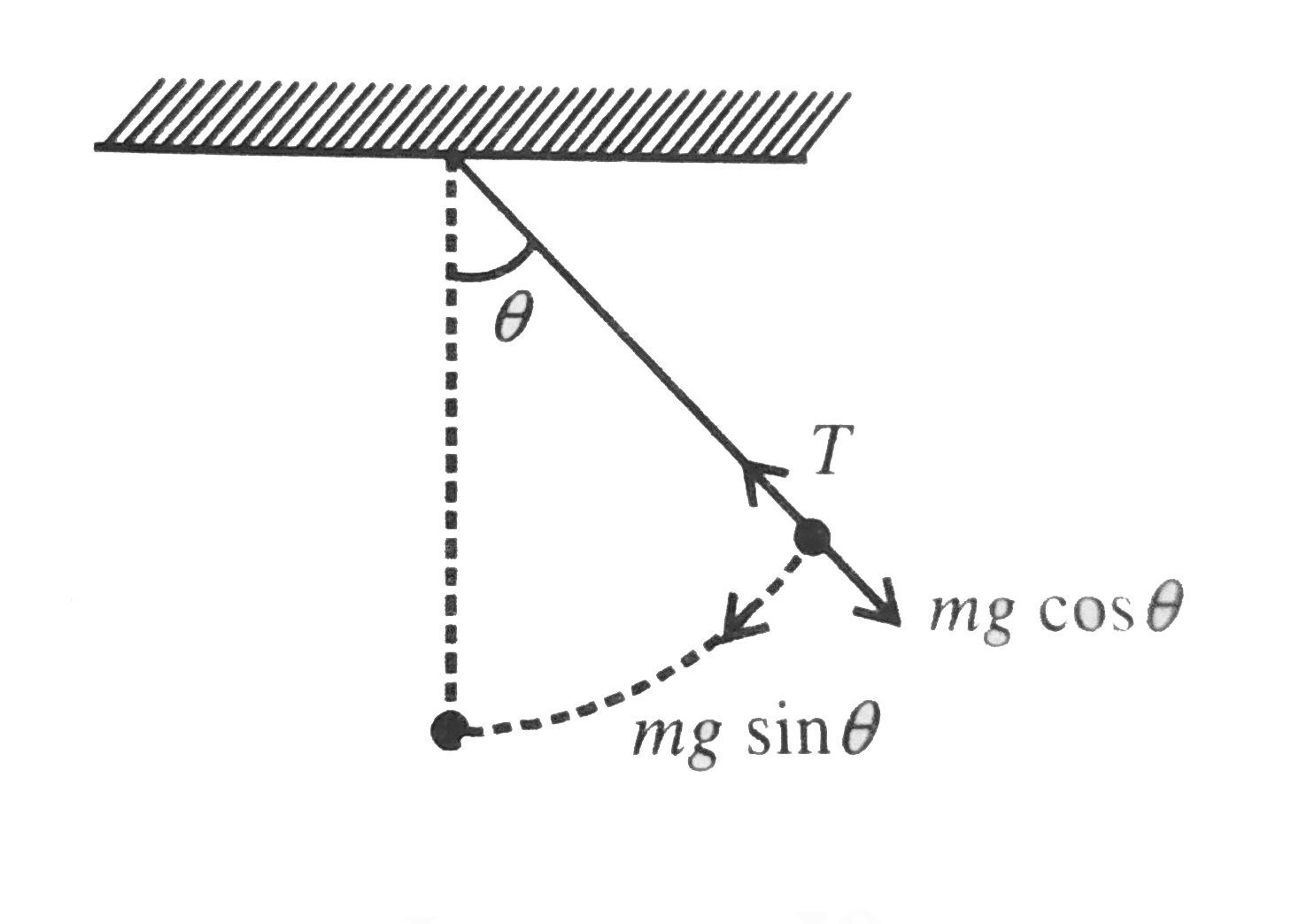
STATEMENT-1 : In simple pendulum performing $S . H . M$ ., net acceleration is always between tangential and radial acceleration except at lowest point.
STATEMETN-2 : At lowest point tangential acceleration is zero.

A

Statement I is true statement II is true, Statement II is a correct explanation for Statement I.

B

Statement I is true statement II is true, Statement II is NOT a correct explanation for Statement I.

C

Statement I is true, Statement II is false

D

Statement I is false, Statement II is true

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$T - m g \cos θ = \frac{m v^{2}}{r} \Rightarrow m g \sin θ = F_{T}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
when a body performs a U.C .M Its tangential acceleration is
A $\frac{v^{2}}{r}$
B $\frac{v}{r^{2}}$
C $\frac{v}{r}$
Dzero
Question 2 - Select One
A particle is performing a U.C .M along a circular path of radius r, with a uniform speed v. Its tangential and radial acceleration are
Azero and infinite
B $\frac{v^{2}}{r}$ and zero
Czero and $\frac{v^{2}}{r}$
D $r ω^{2}$ and infinite
Question 3 - Select One
In previous problem, the tangential acceleration of a point on the rim is :
A $\frac{T}{M}$
B $\frac{M R^{2}}{T}$
C $\frac{2 T}{M}$
D $\frac{M R^{2}}{2 T}$

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Assertion Reasoning

Home
Ask Doubt
Profile