Question

A particle performing simple harmonic motion undergoes unitial displacement of $\frac{A}{2}$ (where A is the amplitude of simple harmonic motion) in 1 s. At $t=0$, the particle may be at he extreme position or mean position the time period of the simple harmonic motion can be

Options

A. 6s
B. 2.4s
C. 12s
D. 1.2s

Answer

A::C

Explanation

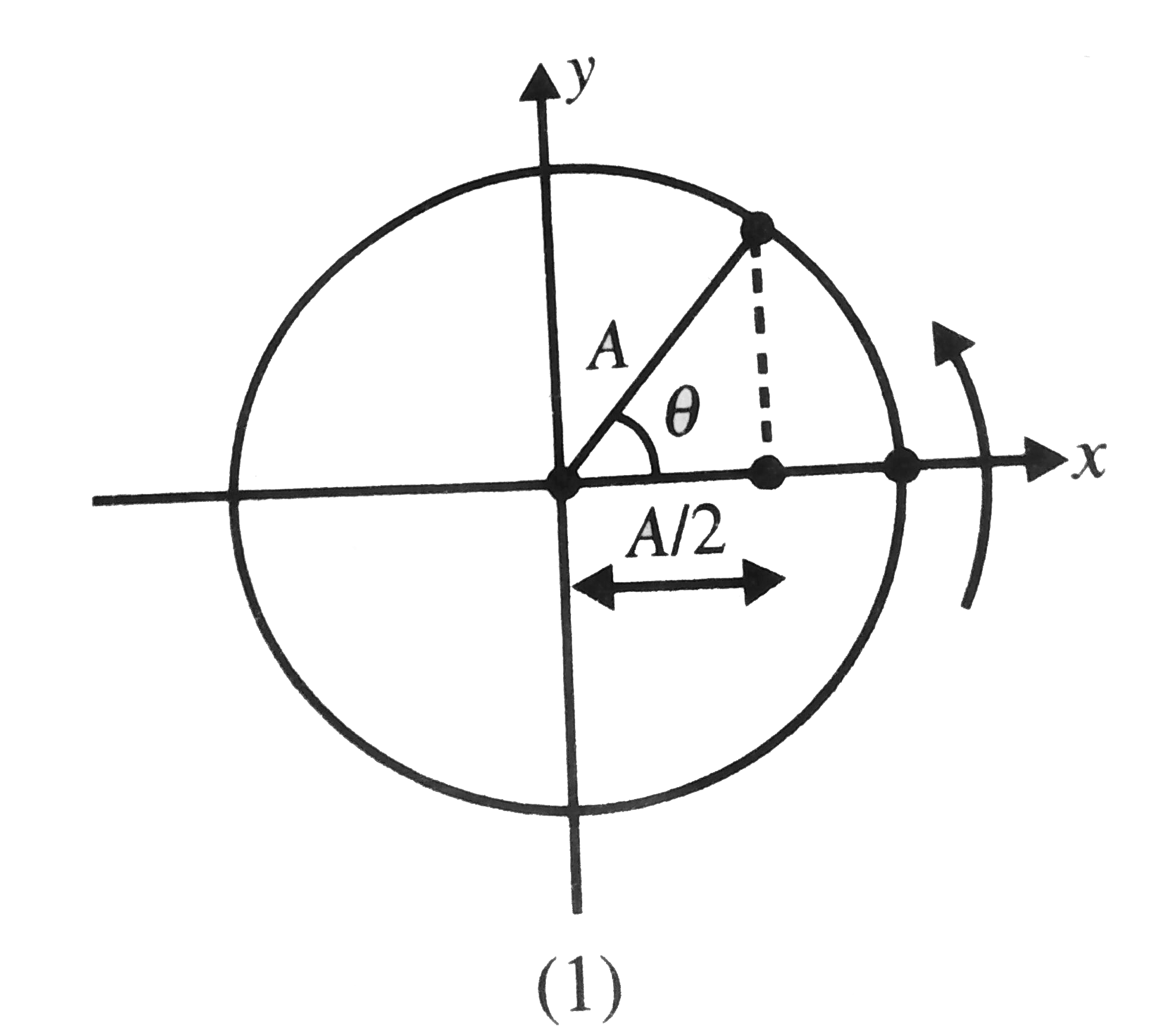
At `t=0` when particle is at extreme position, the situation is as shown Fig.
From the figure `costheta=((A)/(2))/(A)=(1)/(2)`
`theta=(pi)/(3)implies(pi)/(3)=(2pi)/(T)xx1impliesT=5s`
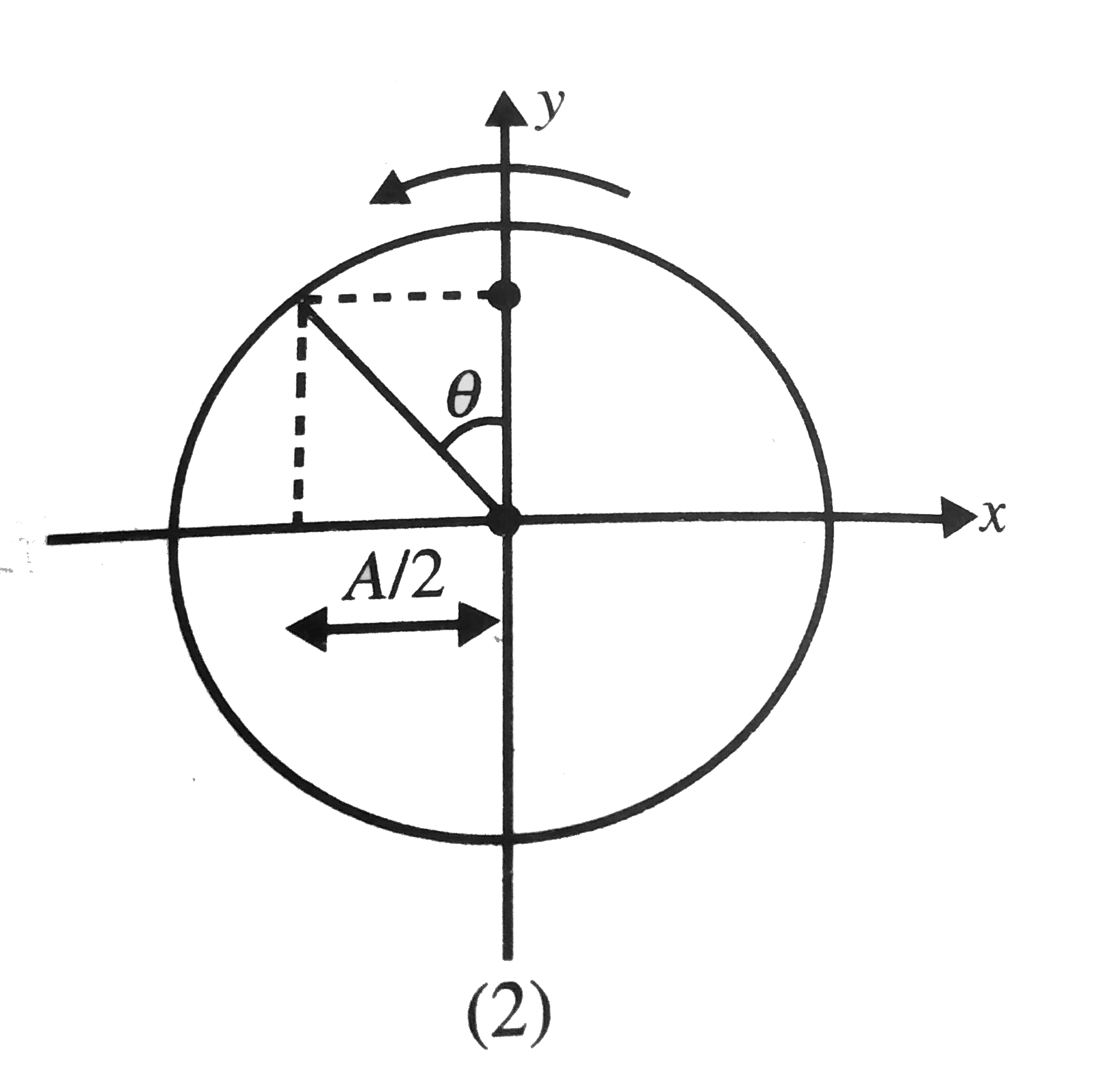
At `t=0` when particle is at mean position the situation is as shown fig.
From the figure. `sintheta=((A)/(2))/(A)`
`theta=(pi)/(6)`,but `theta=omegatimplies(pi)/(6)=(2pi)/(T)xx1impliesT=12s`
If initially the particle is located somewhere else, then time period comes out to be different A reverse question can also be formed on the same concept.