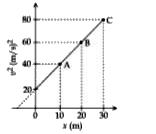
In problem 9 the acceleration of the particle is
A
and
B
and
C
and
D
and
Video Solution
Text Solution
The correct Answer is:C
From the graph
(distance between the two adjacent shown in the figure)
and ,
m
Also
The equation of velocity can be written as
At extreme position, , or
Phase of the particle velocity at that insstant corresponding to the above equation
Therefore, when a phase change of takes place, the resulting phase
(numerically)
Since at , the particle is at the extreme position, there fore at ,
Clearly a phase change of corresponds to a time difference of
(numerically)
Acceleration
at
Maximum displacement
and maximum accceleration,
|
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
Knowledge Check
A particle revolves round a circular path with a constant speed the acceleration of the particle is :
Aalong the circumference of the circleBalong the tangentCalong the radiusDzeroTwo particles of equal mass have velocities and . First particle has an acceleration while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of
Astraight lineBparabolaCcircleDellipseWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
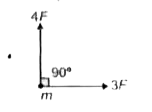 AaB2aC5aD8a
AaB2aC5aD8a
For a particle revolving in a circular path, the acceleration of the particle is
View SolutionA particle revolves round a circular path. The acceleration of the particle is inversely proportional to-
View SolutionA particle is moving in a circle with a constant speed, the acceleration of the particle has
View SolutionA particle revolves round a circular path. The acceleration of the particle is inversely proportional
View SolutionThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
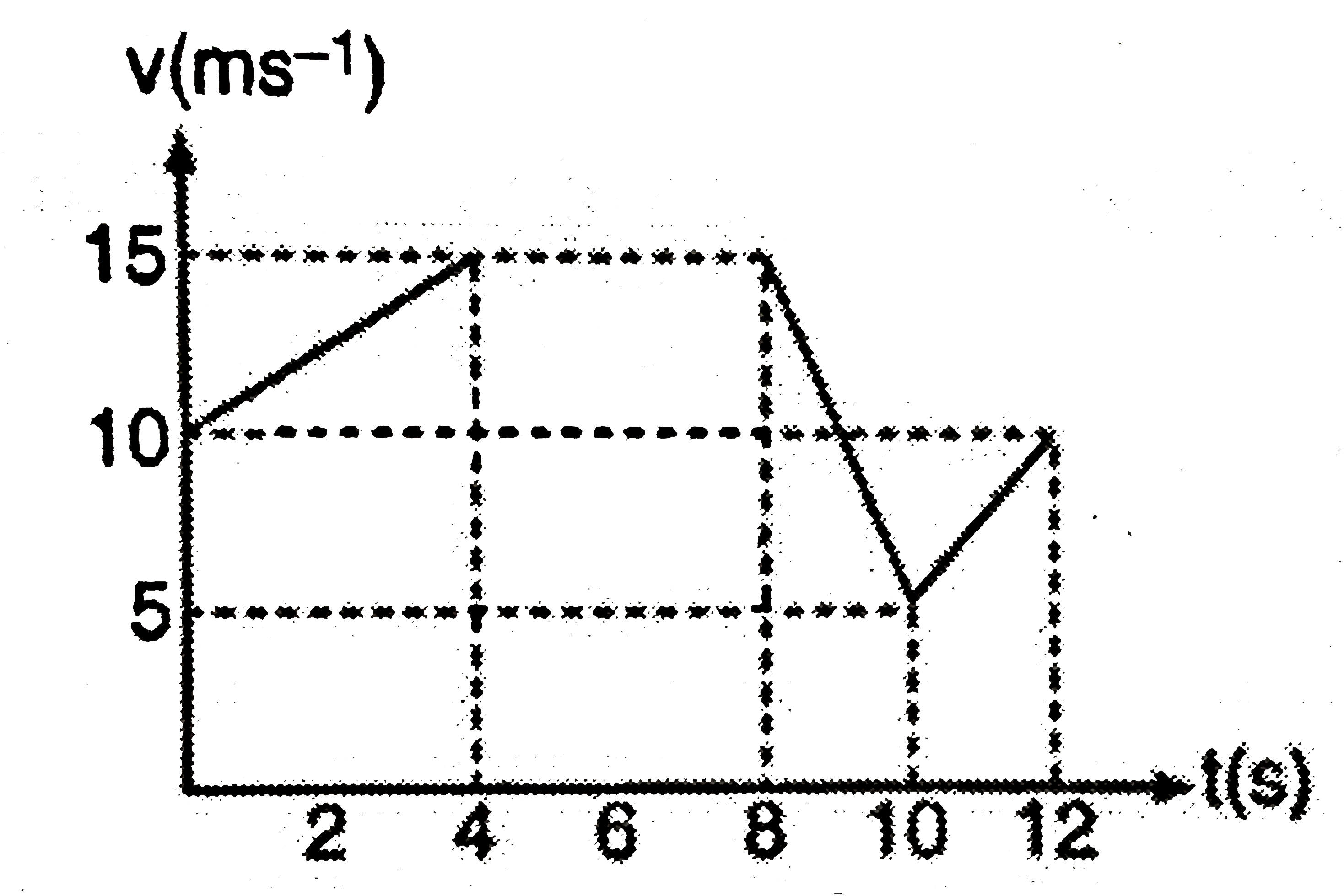
View Solution