A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
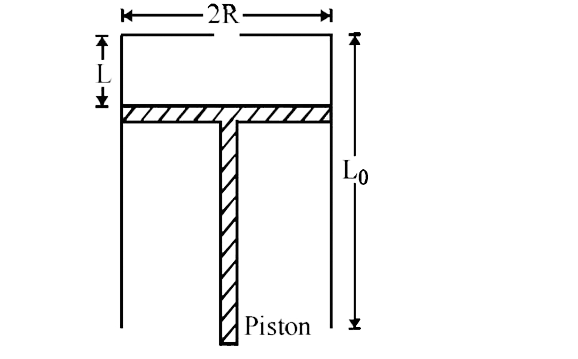
The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is ρ. In equilibrium, the height H of the water coulmn in the cylinder satisfies

ρg(L0−H)2+p0(L0−H)+L0p0=0
ρg(L0−H)2−p0(L0−H)−L0p0=0
ρg(L0−H)2+p0(L0−H)−L0p0=0
ρg(L0−H)2−p0(L0−H)+L0p0=0
The correct Answer is:C
p1=p2
p0+pg(L0−H)=p (i)
Now, applying p1V1=p2V2 for the air inside the cylinder, we have
p0(L0)=p(L0−H)
p=p0L0L0−H
Substituting in Eq. (i), we have
p0+pg(L0−H)=p0L0L0−H
⇒pg(L0−H)2+P0(L0−H)−L0p0=0
Therefore, option (c) is correct.
Topper's Solved these Questions
- ARCHIVES 1 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 1 VOLUME 6EXERCISE - Integer
4 Videos
- ARCHIVES 1 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 1 VOLUME 6EXERCISE - Assertion-Reasoning
1 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer
4 Videos
Similar Questions
_E01_201_Q01.png)
A piston of mass M=3kg and radius R=4cm has a hole into which a thin pipe of radius r=1 cm is inserted the piston can enter a cylinder tightly and without friction an initially it is at the bottom of the cylinder 750 gm of water is now poured into the pipe so that the piston&pipe and lifted up as shown find the height H of water in the cylinder and height h of water in the pipe.
View SolutionA fixed thermally conducting cylinder has radius R and length L0. The cylinder is open at its bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
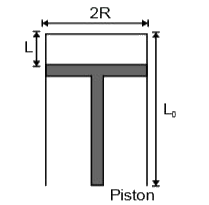
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top is
View Solution
Knowledge Check
The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brough below the cylinder and put in a positoon so that the water surface in the tank is at the same level as the top of the cylinder as shown in the fgure. The density of the water is rho.In equilibriium, the height H of the water column in the cylinder satisfies
 Aρg(L0−H)2+P0(L0−H)+(L0P0)=0Bρg(L0−H)2−P0(L0−H)−L0P0=0Cρg(L0−H)2+P0(L0−H)−L0P0=0Dρ(L0−H)2−P0(L0−H)+(L0P0)=0
Aρg(L0−H)2+P0(L0−H)+(L0P0)=0Bρg(L0−H)2−P0(L0−H)−L0P0=0Cρg(L0−H)2+P0(L0−H)−L0P0=0Dρ(L0−H)2−P0(L0−H)+(L0P0)=0A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
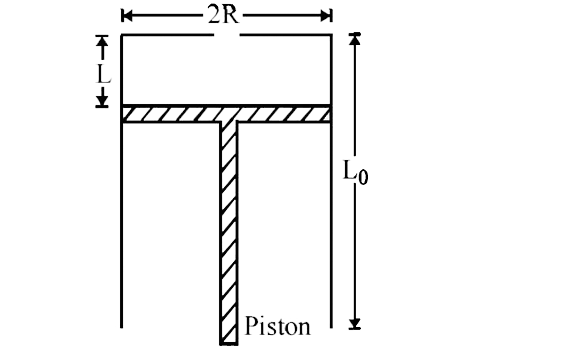
The piston is now pulled out slowly and held at a distance 2L from the top. The pressure in the cylinder between its top and the piston will then beAP0BP02CP02+MgπR2DP02−MgπR2A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
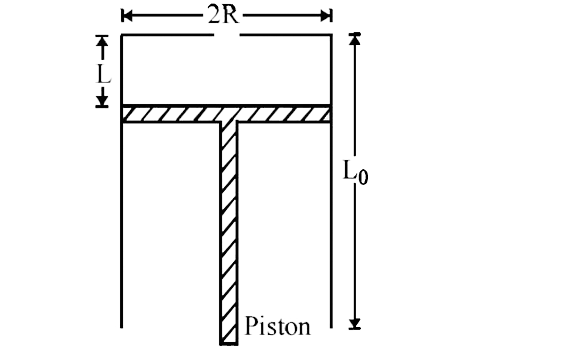
While the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a position where it can stay in equilibrium. In this condition, the distance of the piston from the top isA(2P0πR2πR2P0+Mg)(2L)B(P0πR2−MgπR2P0)(2L)C(P0πR2+MgπR2P0)(2L)D(P0πR2πR2P0−Mg)(2L)
The volumes of a sphere and a right circular cylinder having the same radius are equal. The ratio of the diameter of the sphere to the height of the cylinder is
View SolutionA sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is 4π r3 (b) 83π r3 (c) 2π r3 (d) 8π r3
View SolutionWhile the piston is at a distance 2L from the top, the hole at the top is sealed. The piston is then released, to a poistion where it can stay in equilibrium. In this condition, distance of the piston from the top is
View SolutionThe piston I s now pulled out slowly and held at a diatance 2L from the top. The pressure in the cylinder between its top and the piston will then be
View SolutionThe height 'h' and radius 'r' of a right circular cylinder which is open at the top and has a given surface area, will have the greatest volume if
View Solution
