A certain ideal gas undergoes a polytropic process PVn = constant such that the molar specific heat during the process is negative. If the ratio of the specific heats of the gas be γ, then the range of values of n will be
0<n<γ
1<n<γ
n=γ
n>γ
The correct Answer is:B
b. Since PVn= constant and also PV=RT, taking 1 mol of the gas from simplicity
dU=CvdT
Where Cv→ molar specific heat at constant volume.
Now the molar specific heat in a polytropic process PVn= constant is given by
Cv=(Rγ−1)−(Rn−1)=(n−γ)R(n−1)(γ−1)
For this equation we see that Cv will be negative when n<γ and n>1, simultaneously i.e., 1<n<γ. Since γ for all ideal gases is greater than 1, if n>γ or n<1, then Cv will be positive.
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects29videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning6videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective22videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
An ideal gas undergoes a polytropic process PV^(n)= constant,such that the molar specific heat during "],[" the process is negative.If the ratio of the specific heats of the gases be Y,then the range of value of n will be
View SolutionP-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
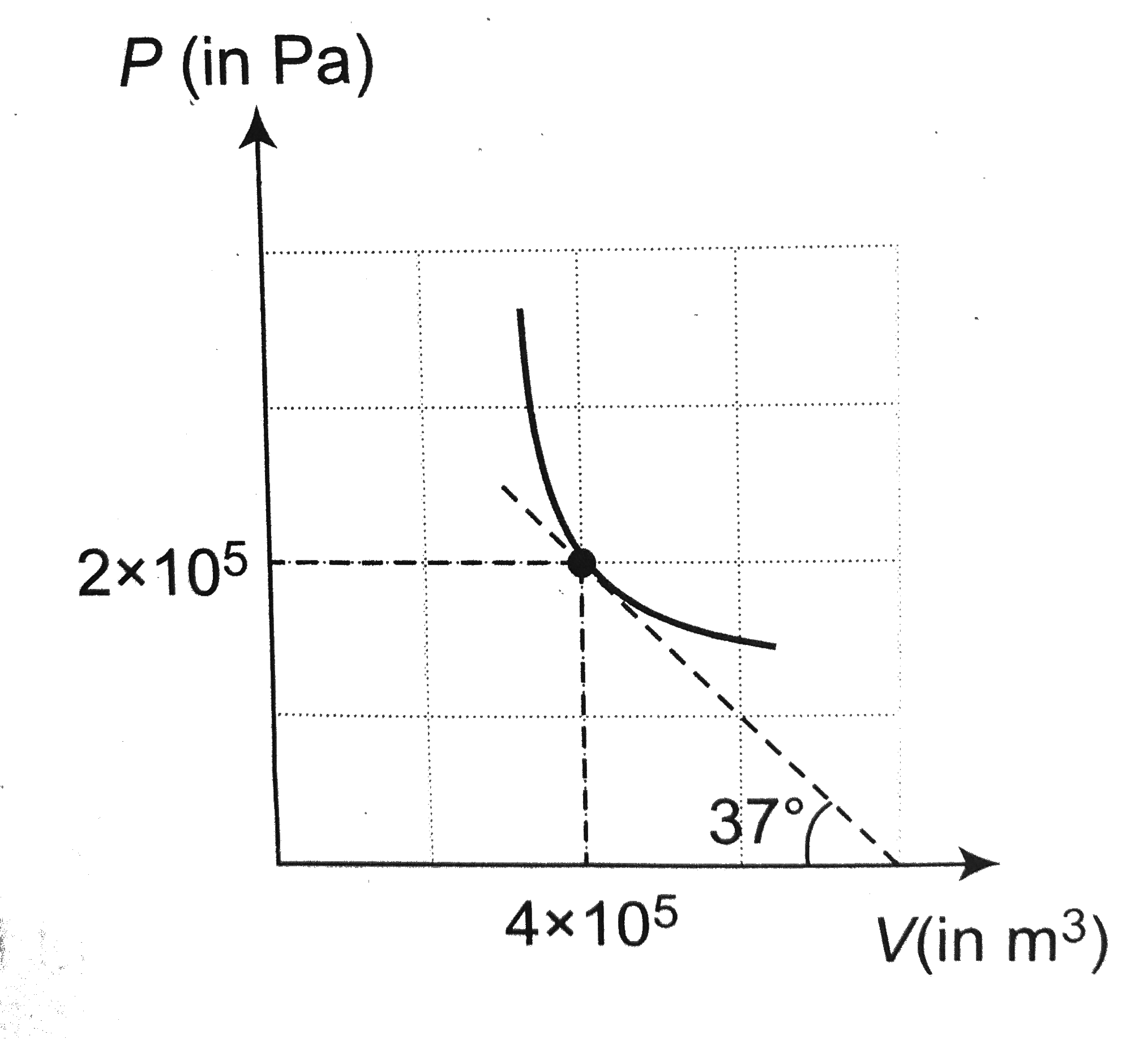 View Solution
View SolutionIf a gas has n degrees of freedom ratio of specific heats of gas is
View SolutionAt constant volume, the specific heat of a gas is 3R2 , then the value of 'γ' will be
View SolutionIf the specific heat of a gas at constant volume is 32R, then the value of γ will be
View SolutionA certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
View SolutionThe specific heat of a gas in an isothermal process is
View SolutionOne mole of an ideal monoatomic gas undergoes a described by the equations PV3= constant The heat the gas during this process is :
View SolutionFor a certain gas the ratio of specific heats is given to be γ=15, for this gas
View SolutionThe specific heat of a gas in an isothermal process is
View Solution


