Six grams of hydrogen gas at a temperature of 273 K isothoermally expanded to five times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. Find the total amount of heat absorbed by the gas during the entire process.
The processes represent on the P-V diagram by the curve 1 to 2 (isothermal) and the line 2 to 3 (isochoric), Here
P1=P3
For the process 1 to 2 (isothermal)
T2=T1,V2=5V1
ΔH=ΔU+W=0+W
⇒ΔH=2.303nRT1log(V2V1)
ΔH=2.303×(62)×8.3×273×log5=10942.4J
State 1 and state 3 are at the same pressure.
⇒V1T1=V3T3⇒T3=V3V1T1=5×273=1365K
Process 2 to 3 : ΔH=ΔU+W
⇒ΔH=nCVΔT+0
ΔH=62×52R×(T3−T2)
⇒ΔH=7.5×8.3×(1365−273)J=67977J
Thus total heat absorbed =ΔH1→2+ΔH2→3=78919.4J
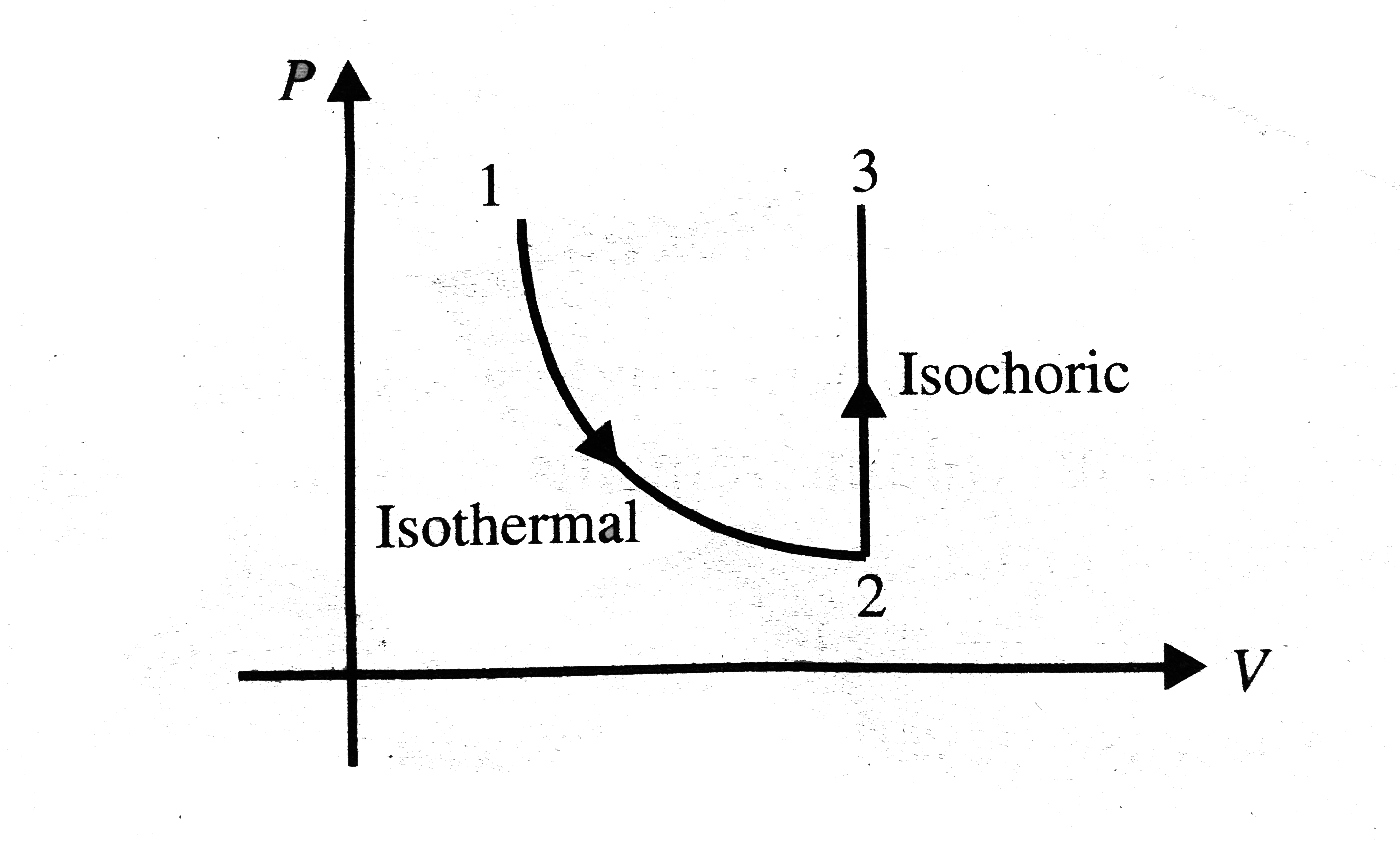
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Solved Examples
Explore 14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Exercise 2.1
Explore 20 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
Similar Questions
Three moles of an ideal gas, initially at T0=273K isothermally expanded n=5 times its initial volume and then isochorically heated so that the pressure in the final state became equal to that in the initial state. The total quantity of heat transferred to the gas during the process was Q=80kJ. Represent the whole process in a pV diagram. Find the adiabatic exponent of the gas.
View SolutionThree moles of an ideal gas being initially at a temperature Ti=273K were isothermally expanded 5 times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. The total heat supplied in the process is 80kJ. Find γ(=CpCV) of the gas.
View Solution
Knowledge Check
A fixed mass of a gas is adiabatically made to expand to double its volume and then isochorically heated to bring the gas to the original pressure. The ratio of final to initial temperature will be
A1:1B2:1C1:2DDepends on the atomicity of the gas.
Two moles of a certain ideal gas at 300K is cooled at constant volume so that the pressure is reduced to half the original value. Now the gas is heated at constant pressure so that its temperature becomes equal to the initial temperature. Find the total amount of heat absorbed by the gas in the process.
View SolutionTwo moles of an ideal gas at temperature T0=300K was cooled isochorically so that the pressure was reduced to half. Then, in an isobaric process, the gas expanded till its temperature got back to the initial value. Find the total amount of heat absorbed by the gas in the processs
View SolutionTwo moles of a certain ideal gas at temperature T0= 300 K were cooled isochorically so that the gas pressure reduced η= 2.0 times. Then, as a result of the isobaric process, the gas expanded till its temperature get back to the initial value. Find the total amount of heat absorbed by the gas in this process.
View SolutionTwo moles of a certain ideal gas at 300K were cooled at constant volume so that the pressure was reduced to half t he initial value. Then, as a result of heating at constant pressure, the gas expanded till its temperature got back ot the initial value. Find the total amount of heat absorbed by the gas in the process.
View SolutionTwo moles of a certain gas at a temperature T0=300K were cooled isochorically so that the pressure of the gas got reduced 2 times. Then as a result of isobaric process, the gas is allowed to expand till its temperature got back to the initial value. Find the total amount of heat absorbed by gas in this process.
View SolutionOne mole of an ideal gas at temperature T was cooled isochorically till the gas pressure fell from P to Pn. Then, by an isobaric process, the gas was restored to the initial temperature. The net amount of heat absorbed by the gas in the process is
View SolutionWhen 3mole of an idela gas expand reversibly and isothermally five times its initial volume 6kJ heat flow into it. What must be the temperature of the gas?
View Solution

