A thin cylindrical metal rod is bent into a ring with a small gap as shown in figure. On heating the system
A thin cylindrical metal rod is bent into a ring with a small gap as shown in figure. On heating the system

A

θ decreases, r and d increase

B

θ increase

C

d and r increase

D

θ is constant

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C, D

Thermal expansion is like protographic enlargement.

Updated on:21/07/2023
|
Class 11PHYSICSTHERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A metallic rod is bent in the form of ractangle as shown in the given figure and heated .Then the gap between the ends P and Q ______
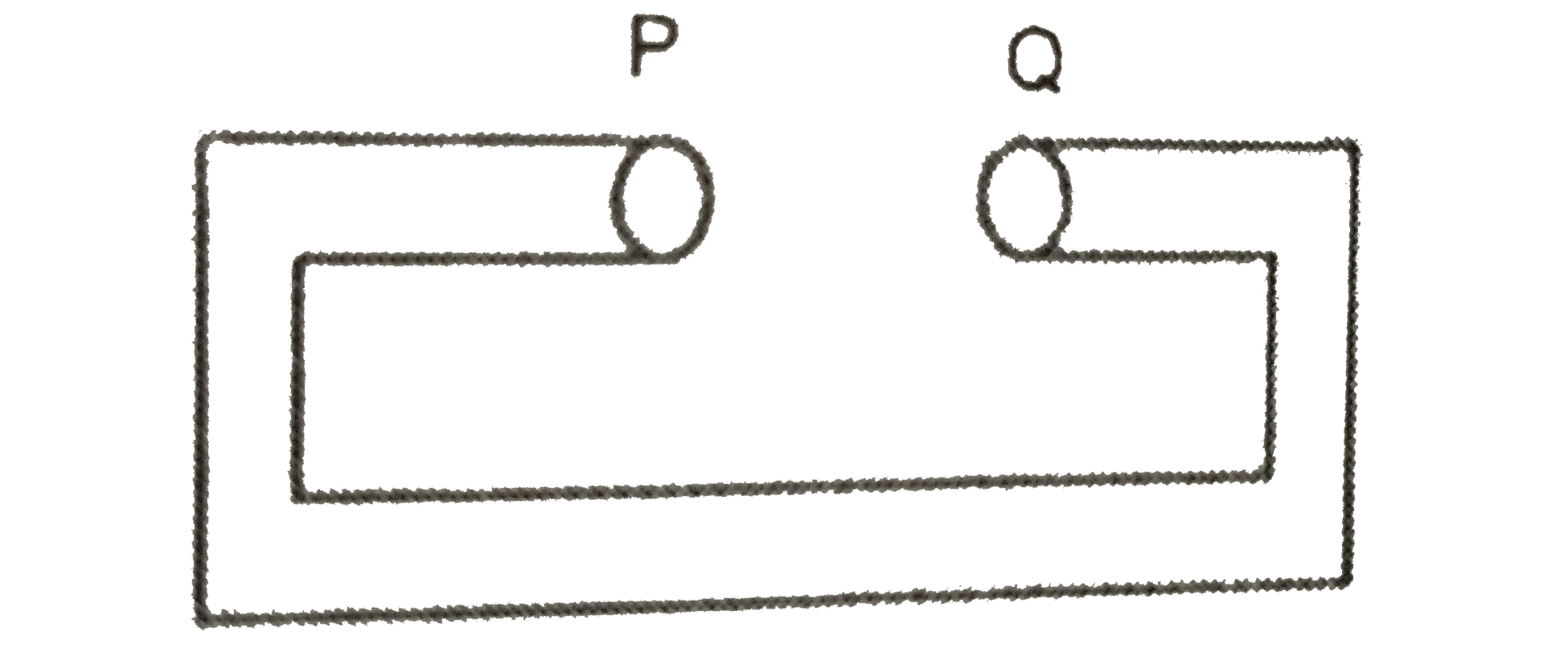    ocr_image

    Aincreases
    Bdecreases
    Cremains same
    DCannot be determined

  • A metal rod is shaped into a ring with a small gap. If this is heated,
    (i) the length of the rod will increase
    (ii) the gap will decrease
    (iii) the gap will increase
    (iv) the diameter gof the ring will increase in the same ratio as the blength of the rod

    A(i),(ii),(iii)
    B(i),(ii),(iv)
    C(i),(iii),(iv)
    D(ii),(iii),(iv)

  • A metallic rod is bent in the form of ractangle as shown in the given figure and heated .Then the gap between the ends P and Q ______
    ocr_image

    Aincreases
    Bdecreases
    Cremains same
    Dconnot be determined