Consider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
K1A1=K2A2
K2A1=K1A2
K1A1S1=K2A2S2
K2A1S2=K1A2S1
The correct Answer is:A
To solve the problem, we need to analyze the heat conduction through two rods with different properties but equal rates of heat loss. The key concept here is to use Fourier's law of heat conduction, which states that the rate of heat transfer (Q/t) through a material is proportional to the temperature difference across the material and the area, while inversely proportional to the length of the material.
1. Understand the Formula for Heat Conduction:
The rate of heat conduction (Q/t) through a rod can be expressed using Fourier's law:
Qt=K⋅A⋅(T1−T2)L
where:
- K is the thermal conductivity of the material,
- A is the cross-sectional area,
- T1 and T2 are the temperatures at the ends of the rod,
- L is the length of the rod.
2. Set Up the Equations for Both Rods:
For the first rod (Rod 1):
Qt=K1⋅A1⋅(T1−T2)L
For the second rod (Rod 2):
Qt=K2⋅A2⋅(T1−T2)L
3. Equate the Heat Loss Rates:
Since the rate of heat loss is equal for both rods, we can set the two equations equal to each other:
K1⋅A1⋅(T1−T2)L=K2⋅A2⋅(T1−T2)L
4. Cancel Out Common Terms:
The length L and the temperature difference (T1−T2) are common to both sides of the equation and can be canceled out (assuming T1≠T2):
K1⋅A1=K2⋅A2
5. Solve for the Relationship Between Areas and Conductivities:
Rearranging gives us the relationship between the conductivities and the areas:
K1K2=A2A1
Final Result:
The relationship between the thermal conductivities and cross-sectional areas of the two rods is given by:
K1⋅A1=K2⋅A2
The rate of heat conduction (Q/t) through a rod can be expressed using Fourier's law:
Qt=K⋅A⋅(T1−T2)L
where:
- K is the thermal conductivity of the material,
- A is the cross-sectional area,
- T1 and T2 are the temperatures at the ends of the rod,
- L is the length of the rod.
For the first rod (Rod 1):
Qt=K1⋅A1⋅(T1−T2)L
For the second rod (Rod 2):
Qt=K2⋅A2⋅(T1−T2)L
Since the rate of heat loss is equal for both rods, we can set the two equations equal to each other:
K1⋅A1⋅(T1−T2)L=K2⋅A2⋅(T1−T2)L
The length L and the temperature difference (T1−T2) are common to both sides of the equation and can be canceled out (assuming T1≠T2):
K1⋅A1=K2⋅A2
Rearranging gives us the relationship between the conductivities and the areas:
K1K2=A2A1
The relationship between the thermal conductivities and cross-sectional areas of the two rods is given by:
K1⋅A1=K2⋅A2
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Two metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View Solution
Knowledge Check
Condider two rods of same length and different specific heats (s1,s2), thermal conductivities (K1,K2) and areas of cross-section (A1,A2) and both having temperatures (T1,T2) at their ends. If their rate of loss of heat due to conduction are equal, then
AK1A1=K2A2BK1A1s1=K2A2s2CK2A1=K1A2DK2A1s2=K1A2s1Two rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oilAll the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
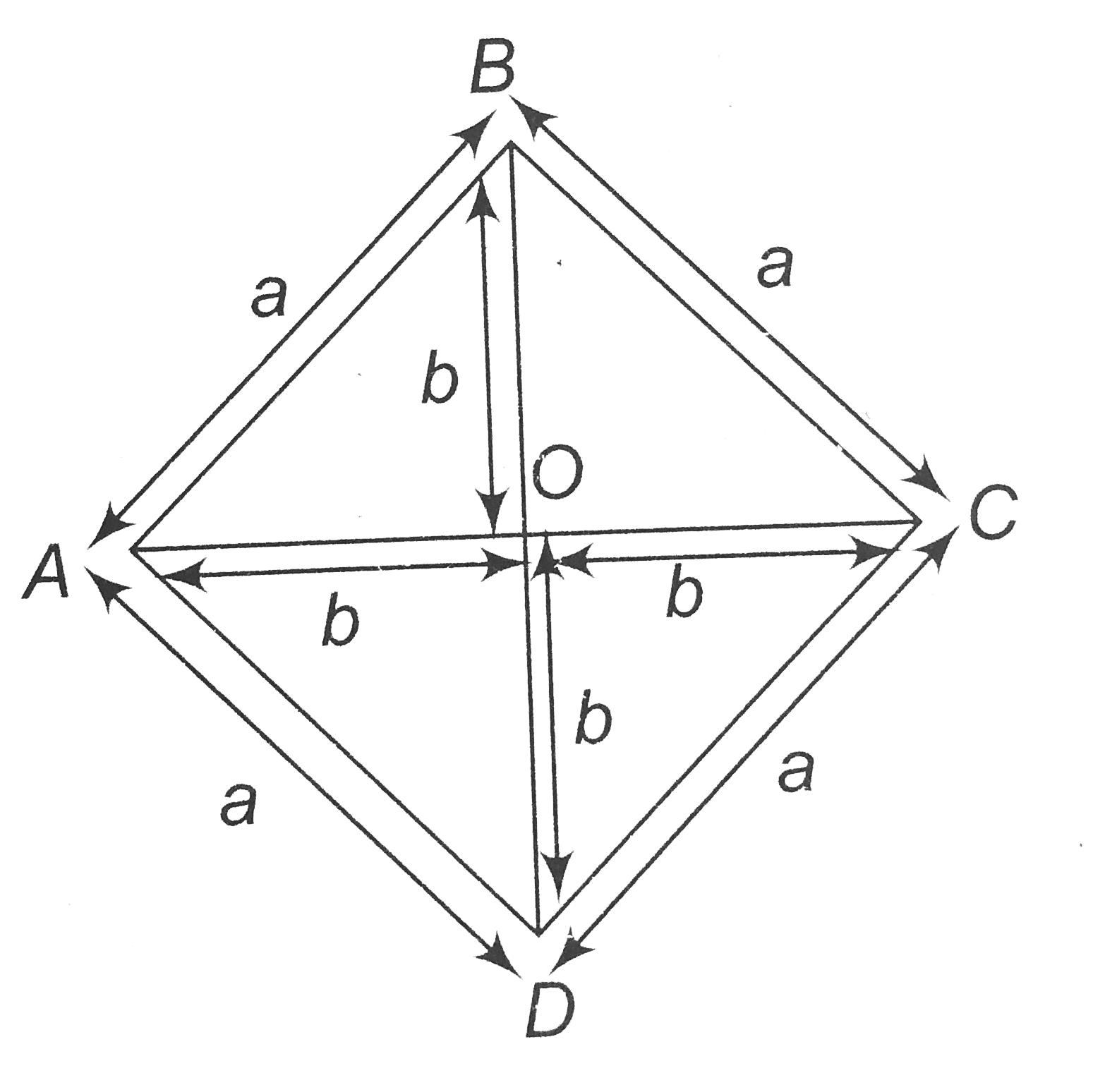 ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
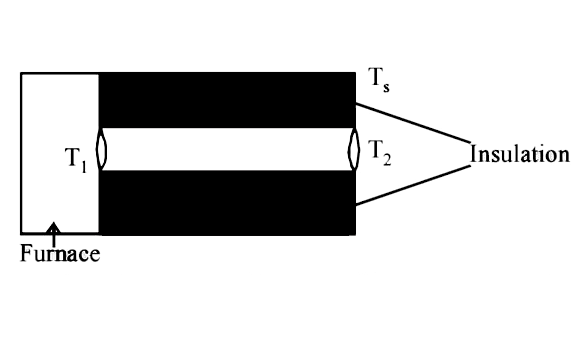
A cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T1 and the other end in surrounding at temperature T2. Surface of the rod exposed to the surrounding has emissivity e. Also T2=Ts+ΔTandTs>>ΔT. If T1−Ts∝ΔT,find the proportionality constant.
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionActivation energy (Ea) and rate constants (k1andk2) of a chemical reaction at two different temperature (T1andT2) are related by
View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View Solution
