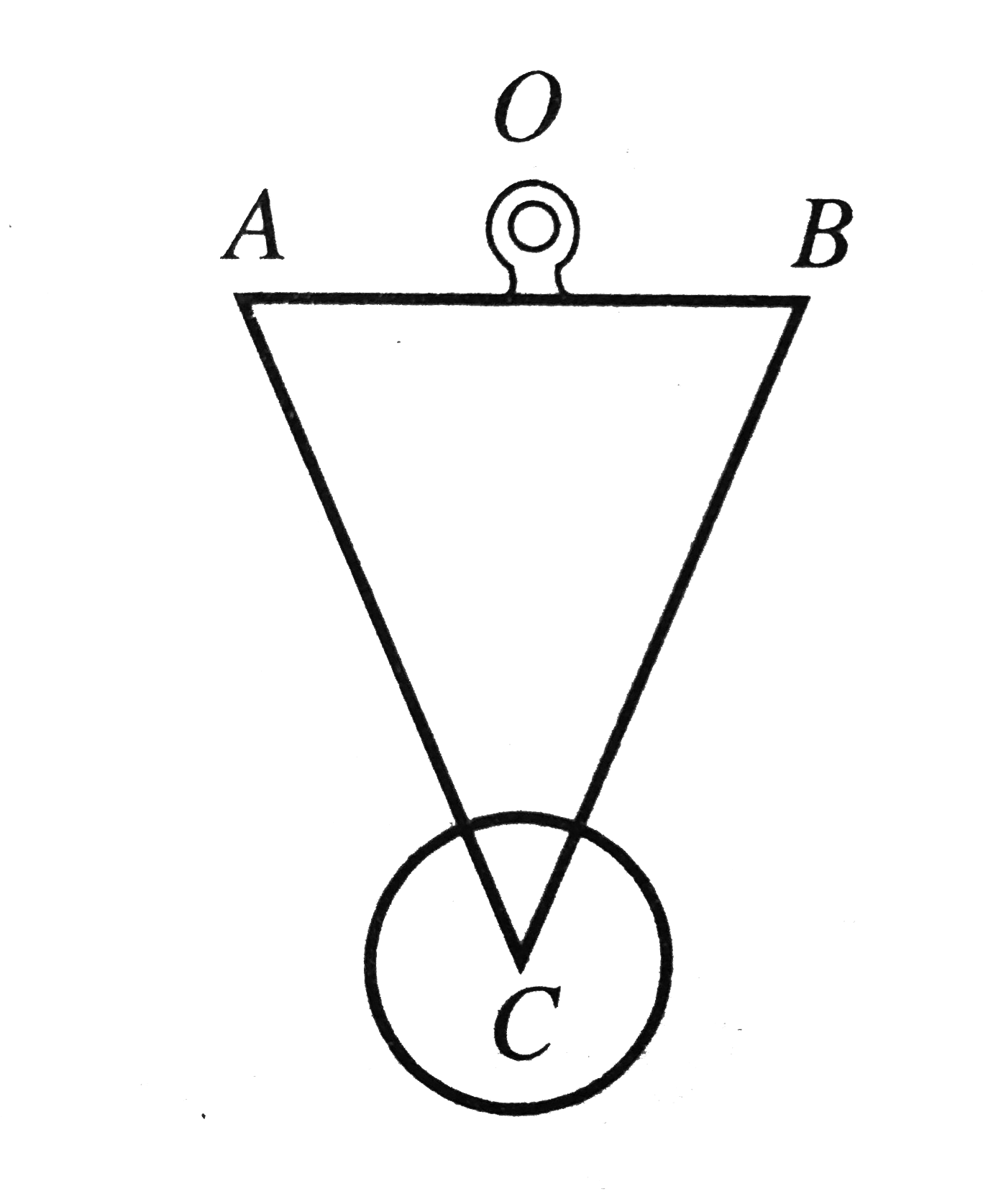
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length cm and coefficent of linar expansion and side length and coefficient of linear expansion . find so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.
First we must know what is a compensated pendulum. We've dicussed that due to change in temperature the time period of a pendulum clock changes. Due to this, in pendulum clocks , to make a pendulum some specific metals are used which have very low coefficient of expansion so that the error intriduced in their time is very small. The other alternative of minimizing the error in time measurement, is to use compensated pendulum. This is a pendulum made up of two or more metals as shown in Fig.
In this case the distance of centre of mass from suspension point O is
When temperature is changed by , new value of h will become
As we require , we have
or
or .
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Single Correct148videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Multiple Correct25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.318videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
A rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionAn isosceles triangle is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is
 View Solution
View SolutionThere are two rods of length l1 l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.View SolutionIf L1 and L2 are the lengths of two rods of coefficients of linear expansion α1 and α2 respectively the condition for the difference in lengths to be constant at all temperatures is
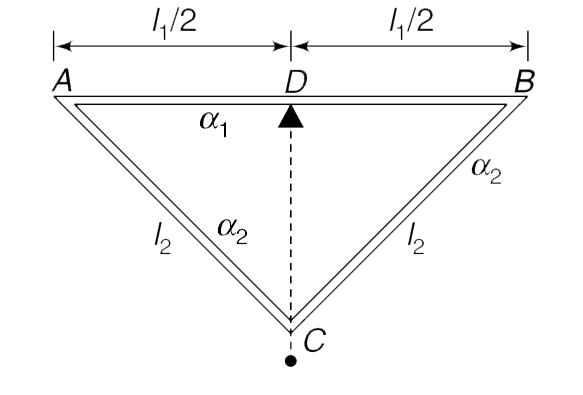
View SolutionIn a compensated pendulum a triangular frame ABC is made using two different metals. AB of length l1 is made using a metal having coefficient of linear expansion α1. BC and AC of length l2 each have coefficient of linear expansion α2. A heavy bob is attached at C. Pendulum can oscillate about the pivot D. Find l2l1 so that distance of bob from the pivot point D does not change with change in temperature.
 View Solution
View SolutionThe compensated pendulum of a clock consista of an isosceles triangular frame of base length l1 and expansivity α1 and side length l2 and expansivity α2. The pendulum is supported as shown in the figure. Calculate the ratio l1/l2 so that the length of the pendulum may remain unchanged at all temperatures?
 View Solution
View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View SolutionAmong three rods, the first two are made of same material having coefficient of linear expansion α1 and the third rod is made of material of coefficient of linear expansion α2 . The third rod forms the base of the equilateral triangle when the three rods are arranged to form an equilateral triangle. If the altitude of triangle remains constant at all temperatures, what is the ratio of α1/α2 ?
View SolutionThe length of a brass rod is 1.5 m. Its coefficient of linear expansion is 19×10−6K−1 Find the increase in length of the rod if it is heated through 20∘C.
View Solution


