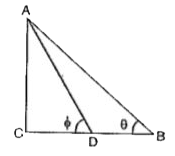
In the previous problem, if $(ϕ)$ is the angle between line of emergence DE and normal DF at point D, ratio of $(ϕ) / (θ)$ for positive value of $(θ)$ will be

A

$1$

B

$> 1$

C

$< 1$

D

depands upon $\to B$ and charge

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The geometry i=of the figure of the solution of problem (22) suggests $ϕ = θ$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34videos
MISCELLANEOUS VOLUME 5
BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84videos
MISCELLANEOUS VOLUME 5
BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3videos
MISCELLANEOUS VOLUME 3
BOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20videos
Moving charges and magnetism

Similar Questions

Knowledge Check

Question 1 - Select One
In the relation $ϕ = B A cos θ, θ$ is angle
Awhich normal to surface area makes with the direction of magnetic field
Bwhich magnetic field makes with the surface
Cwhich is never constant
Dnone of the above
Question 2 - Select One
If tan $θ = 1 and sin ϕ = \frac{1}{\sqrt{2}}$ , then the value of $cos (θ + ϕ)$ is
A $- 1$
B0
C1
D $\frac{\sqrt{3}}{2}$
Question 3 - Select One
If $2 sec 2 θ = tan ϕ + cot ϕ$ , then one of the values of $θ + ϕ$ is
A $\frac{π}{2}$
B $\frac{π}{4}$
C $\frac{π}{3}$
Dnone of these

CENGAGE PHYSICS-MISCELLANEOUS VOLUME 5-Integer

Home
Ask Doubt
Profile